Comptes Rendus MATh.en.JEANS 04-01

 

Des carrés dans les rectangles

 

par

BENDIAB Eddine(4éme), BOFFELLI Anaïs(4éme), CONNAN Laëtitia(4éme), GUILLOT Mathieu (6éme ),
KOCH Tom (4éme), LACOSTE Arthur (3éme), LEROUX Jérome(4éme), MONTAY Romain (4éme),
PELLETIER Mélanie(3éme), SANTAMARIA Adrien (4éme) etTELLIER Yoann(4éme).

des collèges L'Ardillière de Nézant à St Brice (Val d'Oise) et Charles Lebrun à Montmorency (Val d'Oise).

Enseignants : Yann BOURIT, (St-Brice) et Christian GEORGES (Montmorency).

Chercheur : François PARREAU (Inst. Galilée, Univ. Paris 13, 93-Villetaneuse).

Jumelage MATh.en.JEANS entre les collèges Charles Lebrun à Montmorency et L'Ardillière de Nézant à St Brice (95, Val d'Oise). Ateliers de Pratique Scientifique, année scolaire 2003-2004.

 

[Article vérifié et annoté : les passages entre crochets sont des éditeurs]

[ L'icone renvoie au Glossaire MATh.en.JEANS , à un document ]

[Résumé. (par les éditeurs) En remplissant pas à pas le mieux possible un rectangle donné avec des carrés, on trouve des fractions successives dont les valeurs se rapprochent du rapport entre la longueur et la largeur du rectangle. ]

MOTS CLEFS
FORME / PROPORTION / FRACTION CONTINUE / NOMBRE RATIONNEL / NOMBRE IRRATIONNEL / RECTANGLE / CARRÉ / ANTYPHÉRÈSE / RACINE CARRÉE / FORMAT DE PAPIER / DÉCOUPAGES / PLIAGES / APPROXIMATION

Plan

0- Présentation du sujet, par les auteurs, par le chercheur
1- Passage de la fraction au codage
2- Passer du code à la fraction (A. Exemple du code 3-2-5 B. Formules et exemple plus long).
3- Comparaison de codes (conjecture 3.1 A. Exemple : 1-3 et 1-2 B. Exemple : 1-2-2 et 1-2-3 C. Testez )
4- Le code infini [pour racine de 2] A. Introduction B. Démonstration)
-   notes des éditeurs et documentation sur le sujet

[0. Le sujet]

Le but du jeu est de découper l'aire du rectangle en différents carrés à l'aide de découpages sucessifs.

Nous allons vous donner un exemple.

Nous décomposons un rectangle 16/9 (c'est à dire 16 de longueur et 9 de largeur) en différents carrés.

Le premier carré est coupé dans la longueur initiale (de 16) du rectangle il est de 9 sur 9.

Il va nous rester un rectangle de 7 de largeur et 9 de longueur, nous redécoupons un carré dans la nouvelle longueur, il sera donc de 7 sur 7.

Ensuite nous obtenons un nouveau rectangle d'une longueur de 7 et une largeur de 2. Nous refaisons des pliages pour avoir 3 carrés de côté 2.

Et [avec un dernier découpage] nous obtenons 2 carrés de 1.

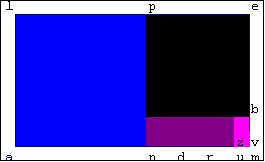Le code est 1-1-3-2 car ont peut placer :

-->tout d'abord

1 seul carré dans la longueur initiale

--> puis

1 seul dans la largeur initiale
    [la longueur du rectangle restant].

--> ensuite on peut en placer

3 dans la largeur du second rectangle obtenu
    [la longueur du rectangle restant].

--> et

2 dans la longueur du second [quatrième] rectangle.

L'espace est totalement occupé, le codage est donc fini.

[Les questions étudiées]

 

[Les résultats présentés dans l'article suivent le plan proposé par les questions initialement posées par le chercheur

Questions :

 Voir le texte complet du sujet proposé par le chercheur]

Comptes Rendus MATh.en.JEANS 04-01 

© MATh.en.JEANS 2004. Tous droits réservés.

début     page suivante    

début d'article

page suivante

notes des éditeurs

Retour aux Comptes Rendus MATh.en.JEANS