Des carrés dans les rectangles, Comptes Rendus MATh.en.JEANS 04-01

4. Le code infini

4A. Introduction

On s'est aperçu que les codes de forme 1-2-2-2 ... avec un nombre infini de « 2 » donne un rapport qui tend vers.

Selon s'il y a un nombre pair ou impair de « 2 », le nombre trouvé est supérieur ou inférieur à .

Plus le code comporte de « 2 », plus le nombre trouvé se rapproche de .

Nous pensons qu'un nombre infini de « 2 » donne pour rapport .

Nous avons donc essayé de prendre le problème à l'envers en tentant de démontrer que :

[Théorème 4.1]. Un rectangle dont le rapport longueur/largeur est a pour codage 1-2-2-2... avec une infinité de « 2 ».

4B. Démonstration

Ce dessin a pour proportion 17/12 mais on imagine que cette proportion est de 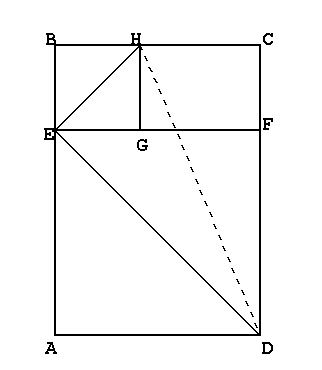(on fait comme si 17 était exactement égal à 12).

On applique le théorème de Pythagore au triangle ADE, rectangle et isocèle en A, en supposant que AD = 1. Ce qui nous permet de déterminer DE (DE2= AD2+AE2 = 12+12 = 2 , d'ou DE = ). Comme on a supposé que DC est égal à , on sait maintenant que DE=DC. Il est donc possible de replier le point C sur le point E, reste à déterminer où se trouvera le pliage. En pliant C sur E, il faut reporter l'angle droit de C en E. On peut ainsi déterminer le pliage (DH), H étant le point d'intersection entre (BC) et la médiatrice de [EC]. On obtient donc un carré EBHG car l'angle HEB vaut 45°, ce qui provient de [la différence entre] l'angle HED qui vaut 90° (comme symétrique de HCD) et l'angle FED qui mesure 45°.   Récapitulation: [Après découpage d'un carré sur la largeur du rectangle initial et d'un carré sur la nouvelle largeur du rectangle restant, il reste le rectangle GHCF]

Donc si un [le] rectangle [GHCF] dans ABCD a les mêmes proportions, alors celui-ci aura le même développement que ABCD et [donnera lieu, après découpages successif de deux carrés, à un nouveau ] rectangle de même proportion et ainsi de suite...

La proportion du rectangle ABCD vaut . Calculons donc le rapport du rectangle GHCF et voyons si il vaut.

EB = BH = HG = GE = AB ; AE = -1 (car AB = et AE=AD=1)

Donc GH = -1

HC = BC ;
HB = 1 - (-1)

donc HC = 2-=(-1).

Et donc

ce qui signifie que le rectangle HCFG a les mêmes proportions que ABCD.

On peut recommencer autant de fois qu'on veut... (note 3).

***

FRACTION CONTINUE / NOMBRE RATIONNEL / NOMBRE IRRATIONNEL / RECTANGLE / CARRÉ / ANTYPHÉRÈSE / RACINE CARRÉE / APPROXIMATION / FORMAT DE PAPIER /DECOUPAGE / PLIAGE

---

Comptes Rendus MATh.en.JEANS 04-01

© MATh.en.JEANS 2004. Tous droits réservés.

précédente        début de page       notes des éditeurs    

début d'article

page précédente

notes des éditeurs

Retour aux Comptes Rendus MATh.en.JEANS

---