---

Préface Ce glossaire est en perpétuelle évolution. Il tente de donner des termes mathématiques utilisés dans les ateliers de recherche et plus généralement dans le site, une définition à la fois - accessible à tous et - suffisamment rigoureuse pour vous permettre de faire vous-même des mathématiques. Il s'agit évidemment d'une "mission impossible" : nous l'avons acceptée en faisant deux hypothèses et un pari : Avertissement (qu'il vaut mieux lire) Vos commentaires et contributions sont bienvenues Consultez le chantier ou écrivez-nous

Mode d'emploi Les mots en italiques sont pris dans leur sens mathématique. Il apparaissent en bleu là où ils sont définis intuitivement et en rouge là où ils sont définis rigoureusement. Lorsque le sens d'un mot particulier est nécessaire ou très utile à la compréhension, un lien renvoie à sa définition. Les mots ou passages signalés par une astérisque (*) sont empruntés au langage mathématique plus spécialisé : il n'est pas nécessaire de les connaître pour comprendre le texte. Le signe ouaccompagne les définitions qui sont encore en chantier. Le signe envoi à un document plus détaillé.

---

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

Symboles

Liste des entrées : un lien (bleu souligné) renvoi à une définition disponible.

absurde (preuve par l' -, raisonnement par l' -)
addition
adjacentes (suites -)
aire
algébrique
algébrique (nombre)
algorithme
angle
anneau
antisymetrie, antisymétrique (relation -)
arête (d'un polygone, d'un polyèdre)
associatif
axiome

barycentre
Bézout (théorème de -) : voir premiers entre eux
Bézier (Pierre - ; 1910-1999)
Bézier (courbe, surface de -)
bijectif (application, correspondance, fonction),
bijection
binôme (formule du - de Newton))
binomial (coefficient - )
bord

cardinal, cardinalité (d'un ensemble)
carré (figure géométrique)
carré parfait, carré (nombre)
cartésien (produit)
cartésien (repère)
Catalan (nombres de -)
classe
collection
commutatif
combinaison
concaténation
conique (courbe, section -)
conjecture
continu (puissance du -)
continue (fonction -)
contraposée (proposition -)
converge (suite qui -)
convergente (suite -)
convexe (polygone, polyèdre, corps)
coordonnées barycentriques : voir barycentre
correspondance
couper
couple
courbe
courbe de Jordan
croisé (polygone - ) : voir polygone

décimal (système, développement, écriture), décimale
décimal (nombre)
décomposition en facteurs premiers : voir premier (facteur)
définition
demi-plan
démonstration
dénombrable
dense
déplacement
dérivée (fonction -)
diophantien
distance
divise
diviseur
division
division euclidienne

ensemble
entier
entier naturel
entier relatif
équation
équation diophantienne : voir diophantien
équilibre (point, droite d'-)
équivalence (relation d' - )
équivalents (éléments) : voir équivalence (relation d' - )
espace, espace géométrique
extérieur
euclidienne (division - ) : voir division euclidienne
euclidien
euclidienne (géométrie -)

face (d'un polyèdre)
facteur
facteurs premiers
factorielle
famille
fermé
Fermat
figure (géométrique)
fini
fonction

géodésique
géométrie
graphe
graphes (théorie des -)
gravité (centre de -)

inclus
inclusion : voir inclus
inconnue : voir équation
infini
infini (ensemble -)
injective (fonction, application, correspondance), injection
intérieur (d'un ensemble, d'un triangle, d'une courbe, d'un convexe, etc.)
interne
intersection
inverse (élément -)
inversible : voir inverse
irrationnel
irréductible (fraction -)
isobarycentre

lemme
limite (- d'une fonction)
limite (- d'une suite)
loi (- de composition)
longueur
losange

majorant
méthode de Newton : voir Newton (méthode de -)
minorant
mot
multiplication

^*
n-uple, n-uplet
naturel (nombre -)
Newton (binôme de -)
Newton (méthode de -)
Nim (jeu de -)
nombre
numérique (fonction -)

opération
opposé (élément -, nombre -)
ordre (relation d' -)
ordre (d'un sommet)
ou
ouvert (ensemble)
ouvert (intervalle)

paire
parallèle
paramètre : voir équation, polynôme, courbe paramétrée
partie (d'un ensemble)
Pascal (triangle de -)
permutation
plan
plan,-e
plat, -e
polyèdre
polygone
polynôme
polynomial : voir polynôme
postulat
postulat (5ème postulat d'Euclide)
préfixe
premier (facteur)
premier (nombre)
premiers entre eux (nombres)
primitif (terme -)
produit
produit cartésien : voir cartésien (produit)
puissance du continu : voir continu (puissance du -)
puissance (- d'un ensemble)
puissance (- d'un nombre)
Pythagore (théorème de -)

quadratique
quadratique (résidu - )
quadrature du cercle : voir algébrique (nombre)
quadrilatère
quadrilatère complet
quotient (voir division)

racine (d'un polynôme)
rationnel (nombre)
rectangle
récurrence (principe de -)
réel (nombre)
réflexive (relation - )
région
relatif (entier -) : voir entier relatif
relation
relation binaire
réunion

sécant (droites sécantes, plans sécants)
semblable
somme (- de deux jeux)
sommet
surjectif, surjective (fonction, application, correspondance), surjection
sous-ensemble : voir partie
soustraction
ssi
symétrique (élément - )
symétrique (relation - )

théorème
Topologie, topologique (espace)
transcendant (nombre -)
transformation géométrique
transitive (relation - )
trapèze
triangle de Pascal voir Pascal (Triangle de ^_)

union

variable

SYMBOLES

Procédé de démonstration où, pour prouver une proposition P, on suppose qu'elle est fausse, puis on montre que cette nouvelle hypothèse conduit à une conclusion absurde.

Exemple. Prouvons : Si deux droites (D1) et (D2) sont parallèles à une même droite (D), alors elles sont parallèles entre elles.

Supposons que (D1) et (D2) ne soient pas parallèles : elles auraient donc un point commun P (par la définition de droites parallèles).

Par P il passerait une parallèle à (D) et une seule (axiome "postulat des parallèles"), soit (D'). (D') étant la seule droite passant par P et parallèle à (D) , chacune des droites (D1) et (D2) serait confondue avec (D'). Les droites D1 et D2 seraient donc confondues, donc seraient parallèles : cette conclusion est absurde, car contraire à notre hypothèse.

Notre hypothèse "(D1) et (D2) ne sont pas parallèles" ayant conduit à une contradiction doit donc être rejetée.
De l'ensemble du raisonnement, on conclut que (D1) et (D2) sont parallèles

retour à la liste

Opération entre entiers naturels qui à deux nombres entiers aet bfait correspondre leur somme  a+ b. Par extension, on appelle addition toute opération qui généralise cette addition entre nombres entiers.

• D'un manière formelle, l'addition des entiers naturels se définit à l'aide de l'union d'ensembles disjoints.

On utilise aussi le mot « addition » (ainsi que les mots qui sont usuellement définis à partir cette opération comme : somme, terme, soustraction, opposé etc.) pour désigner une opération (une loi de composition interne) qui est commutative et associative, plus particulièrement lorsque chaque élément admet un opposé, c'est à dire lorsque la soustraction est toujours possible.

Exemples : on parlera de somme et d'addition pour des vecteurs, des applications linéaires, des matrices, des polynômes, des fonctions, des ensembles, ...

On utilise enfin le mot " addition" pour désigner une opération quelconque portant sur les éléments d'un ensemble (une loi de composition interne*), surtout lorsque cette opération est associative et commutative (par exemple dans les groupes abeliens*)

retour à la liste

Donnons nous une suite croissante de nombres réels, ( u_n) (n), et une suite décroissante de nombres réels, ( v_n) (n ),. On dit que ces suites sont adjacentes si

1) Pour tout n, on a u_n < v_n
2) La suite v_n - u_n converge vers 0.

Les segments [ u_n,v_n] sont alors emboîtés (autrement dit, pour n1, chaque segment [ u_n, v_n] est inclus dans le précédent) et leur longueur tend vers 0 quand n tend vers +.

Deux suites adjacentes sont convergentes et ont même limite.

limite

retour à la liste

Nombre qui exprime l'étendue d'une surface : l'aire d'une surface mesure sa "grandeur", sa "taille", par comparaison à celle d'une surface de référence, choisie comme unité d'aire.

L'unité d'aire sera celle d'un carré de coté 1, c'est à dire d'un carré dont le coté est l'unité de longueur. Si l'unité de longueur est notée u, l'unité d'aire sera notée u² (lire « u au carré »).

Ainsi, l'aire d'une surface S représente donc intuitivement le nombre de "carrés-unités" (carrés de cotés 1) qu'il faut pour fabriquer S. Ce nombre est notée aire(S).

L'aire d'un carré de coté c (exprimé avec l'unité de longueur u) est cx c (exprimé avec l'unité d'aire u2)

.

On peut donner une définition rigoureuse des aires pour les surfaces planes(vues comme des parties du plan) en respectant les propriétés suivantes :

• (1) croissance et positivité .
  Plus une surface est étendue plus son aire est grande. Autrement dit si une surface S est contenue dans une autre, S', on a aire(S)aire(S').
  On convient que l'aire d'une surface vide est nulle : l'aire d'une surface quelconque est donc un nombre positif ou nul : aire(S)0. Si U désigne la surface prise pour unité, on a a(U) = 1.
• (2) additivité. Si une surface S est formée de plusieurs morceaux qui ne se chevauchent pas, l'aire de S est la somme des aires de ces morceaux.
• (3) invariance par isométrie. Si une transformation géométrique t conserve les longueurs, alors elle conserve les aires. Autrement dit si t est une isométrie, on a aire(t(S))=aire(S).

On démontre plus généralement que

Si, lors d'une transformation géométrique, les longueurs sont multipliés par un facteur k, alors les aires sont multipliées par k2= kx k

longueur

retour à la liste

L'Algèbre est la branche des mathématiques qui s'intéresse aux opérations. L'adjectif algébrique qualifie tout objet mathématique (un nombre, une formule, une transformation, une structure, une courbe, une surface ...) qui peut être défini ou construit à l'aide d'opérations de base, telles que l'addition (avec éventuellement passage à l'opposé avec un changement de signe) et la multiplication (avec éventuellement passage à l'inverse avec l'usage d'une barre de fraction). L'algébriste cherche à déceler et à comprendre les propriétés des opérations utilisées et en particulier leurs ressemblances avec l'addition et la multiplication usuelles entre nombres.

retour à la liste

Un nombre réel a est dit algébrique si on peut obtenir 0 en combinant ce nombre (éventuellement plusieurs fois) avec des nombres entiers non nuls (positifs, ou négatifs) à l'aide des seules opérations addition et de multiplication.

Par exemple 22/7 et sont des nombres algébriques car :

7 x (22/7) + (-22) = 0       et        ( x ) + (-2) = 0,

Définition équivalente. Un nombre réel est algébrique s'il est racine d'un polynôme non nul à coefficients entiers.

Un nombre qui n'est pas algébrique est dit transcendant. On a démontré que le nombre est transcendant et ainsi prouvé l'impossibilité de "la quadrature du cercle", c'est à dire l'impossibilité de construire géométriquement à la règle et au compas un carré de même aire que celle d'un cercle donné de rayon 1.

Remarque. On peut dans les défintions précédentes remplacer "entier" par "rationnel" sans changer la notion de nombre algébrique : les nombres algébriques sont algébriques sur 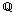(corps des nombres rationnels). Plus généralement, si un corps de nombres K' contient un autre corps de nombres K, on dit qu'un élément de K' est algébrique sur K s'il est racine d'un polynôme non nul à coefficient dans K.

transcendant

retour à la liste

Le mot vient du nom du mathématicien arabe Al Khwarizmi (vers l'an 820), bien que l'idée en soit connue depuis l'Antiquité. Un algorithme est la description d'une suite d'opérations simples, rudimentaires, à effectuer dans un ordre précis pour obtenir, au bout d'un nombre fini d'étapes, un certain résultat.

Exemple. Pour aider un passant égaré, vous lui donnez un algorithme : « Pour la Mairie, continuez tout droit . Au deuxième feu rouge, prenez à droite. Arrivé à la statue tournez à gauche. Marchez jusqu'à un bâtiment rose avec un drapeau national. C'est là. »

Exemple. Pour savoir si un nombre n (entier naturel) est premier, vous pouvez appliquer l'algorithme suivant :

- Comparez n à 1 (étape n°1): si n n'est pas supérieur à 1, arrêtez-vous : n n'est pas premier. Si n est supérieur à 1, continuez de la manière suivante :
- Divisez (à l'aide d'un autre algorithme) n par 2 (2ème étape), puis par 3 (3ème étape), puis par 4 (4ème étape), et ainsi de suite en mémorisant à chaque fois le numéro de l'étape et le reste de la division. Continuez tant que le reste obtenu est différent de 0.
- Lorsque vous obtenez un reste nul à l'étape numéro k, comparez  k à  n. Si k est inférieur à n, arrêtez-vous : le nombre n n'est pas premier, il est divisible par k. Si  k= n, arrêtez-vous : le nombre n est premier.

Dès le début du XXème siècle, avant les premiers ordinateurs, les mathématiciens ont précisé la notion d'algorithme en construisant des machines (imaginaires ou réelles) pouvant effectuer des calculs suivant un plan précis, appelé programme. Ils ont peu à peu identifié les problèmes qui pouvent être résolus par ces machines ; de tels problèmes sont appelés (algorithmiquement) décidables. La branche des mathématiques qui traite de ces questions est la Théorie de la calculabilité*.

retour à la liste

Moyen utilisé, dans le plan ou l'espace, pour parler de l'écartement des deux directions issues d'un même endroit. Dans le plan, on parle d'angle de droites, de segments, de demi-droites, de vecteurs etc., et ces défintions se généralisent à l'espace. Dans l'espace on parle aussi d'angles de plans ou de demi-plans (angles dièdres).

retour à la liste

Ensemble d'éléments pouvant se combiner entre eux grâce à deux opérations ayant des propriétés analogues à l'addition et à la multiplication des nombres entiers relatifs.

Les deux opérations de base dans un anneau sont souvent appelées addition et multiplication, notées respectivement avec les symboles + et ^.  (ou x).

retour à la liste

Côté d'un polygone.
Ligne suivant laquelle deux faces d'un polyèdre se rejoignent, quand elles sont voisines : un cube a douze arêtes. Deux arêtes voisines se rejoignent en un sommet.
Liaison entre deux sommets d'un graphe. (Voir graphes (théorie des))

retour à la liste

Propriété prise pour vraie, avant tout raisonnement.

Grâce aux démonstrations mathématiques, les axiomes et les définitions mathématiques permettent d'obtenir d'autres propriétés vraies, alors appelées théorèmes.

Plus généralement, lorsqu'on travaille dans un cadre particulier, en s'intéressant par exemple à une structure ou à une théorie particulière, on appelle axiomes (de cette structure, de cette théorie), les hypothèses qui permettent de préciser les propriétés des objets de base (termes primitifs) et de raisonner dans ce cadre. Ces hypothèses sont des propriétés que l'on suppose vraies et qui servent de point de départ pour les raisonnements et les démonstrations, pour la construction et la definition de nouveaux objets.

Exemple. Les axiomes de la géométrie plane (euclidienne) précisent le sens et l'emploi des mots de base : points, droites, appartenance d'un point à une droite, longueur, angle, égalité, ....

axiomes de groupe, axiomes des relations d'équivalence, des relations d'ordre, axiomes , de la Topologie de la théorie des probabilités*.

retour à la liste

axiomatique (méthode - )

retour à la liste

Point dont la position est calculée "en faisant la moyenne" entre plusieurs positions plus ou moins importantes. Le mot et la notion de barycentre viennent de la Physique : l'idée est celle de centre d'équilibre de plusieurs masses ponctuelles.

Pour effectuer le calcul, on choisit une origine, on remplace chaque point par le vecteur qui lui correspond (avec O comme origine, le vecteur correspondant à un point M dont le poids est le vecteur, voir espaces affines*), et on multipliant ce vecteur par un coefficient qui exprime l'importance du point considéré (en Physique, ce coefficient sera la masse).

Définition mathématique. Dans le plan, l'espace (et plus généralement dans un espace affine quelconque), le barycentre des points P₁, P₂,..., P_n affecté des coefficients m₁, m₂,...,m_n est l'unique point G qui vérifie l'équation vectorielle:

Quelque soit l'origine O, on a l'égalité :

Coordonnées barycentriques. Lorsque les points P₁, P₂,..., P_n forment un repère affine* (ce qui implique n=2 pour une droite, n=3 pour un plan, n=4 pour l'espace tridimensionnel, etc.) les coefficients m₁, m₂,...,m_n divisés par la somme m=m₁+m₂+...+m_n sont appelés les coordonnées barycentriques du point G : ces coordonnées ne dépendent pas de l'origine O.
une petite introduction au calcul avec des coordonnées barycentriques

Remarque. En Physique, une masse ponctuelle est un point mathématique affecté d'un coefficient (un nombre réel qui mesure la masse). Le centre de gravité G (ou centre d'inertie) d'un système S de n "points massifs" (P₁ , m₁) (P₂ , m₂ ),...,(P_n,m_n) est défini comme le barycentre des points P₁, P₂,..., P_n affecté des coefficients m₁, m₂,...,m_n.

Lorsque chaque point du système est soumis à une force, le déplacement du point G est le même que celui d'une masse ponctuelle unique situé en G, qui serait de masse m=m₁+m₂+...+m_n et serait soumise à une unique force, égale à la résultante (somme vectorielle) des forces appliquées aux divers points.

Si le système est soumis à la seule pesanteur, le centre de gravité est le point d'équilibre du système, en ce sens qu'une force d'intensité m exercée de bas en haut au point G suffit à maintenir l'équilibre. On appelle droite d'équilibre d'un système pesant toute droite par rapport à laquelle le moment résultant* des vecteurs-poids est nul. Ce sont précisément les droites qui passent par G.

retour à la liste

Ingénieur chez Renault, il inventa un procédé pour tracer des courbes à partir de quelques points de base seulement. Les courbes et surfaces de Bézier sont maintenant couramment utilisées dans la Communication et dans l'Industrie (Conception et dessin assisté par ordinateur).

retour à la liste

Une courbe (ou surface) de Bézier est une courbe (ou une surface) définie par quelques points qui permettent de contrôler sa forme.

Dans le plan, une courbe de Bézier sera "le plus simple" des arcs de courbes possibles satisfaisant à un nombre réduit de contraintes : elle devra passer par tel ou tel point , y avoir telle direction, telle courbure... Les surfaces de Béziers sont définies de manière analogue dans l'espace.

. donné et une courbure donné: on voudra que la courbe passe par tel ou tel point, ait telle ou telle direction, ou telle courbure en ces points et tel point, être tangente à telle ou telle droite un morceau de courbe (un arc de courbe) qui est entièrement déterminée par la donnée d'un petit nombre de points, points qui peuvent être sur la courbe (points de tracé) ou hors de la courbe (points de contrôle). Une courbe de Bézier est conçue pour être "la plus simple" des courbes possibles que l'on puisse définir par les points donnés.

Plus généralement on appelle courbe de Bézier : on se donne par exemple les deux points extrémités A et B et on précise la forme (en direction et en courbure) à l'aide d'autres points, non nécessairement sur la courbe.

Exemple : Il existe, en général, une et une seule courbe du troisième degré* reliant deux points donnés A et B et ayant en ces points une direction et une courbure fixées. Cette courbe de Bézier, utilisée dans de nombreux logiciel de dessin, est définie par 4 points A,B,A',B' seulement :

• A et B sont les extrémités de la courbe.
• La courbe est tangente en A à la demi-droite [A,A') et en B à la demi-droite [B,B').
• Plus le point A' est loin de A, plus la courbe est "droite" près de A (autrement la courbure en A est faible). Le point B' contrôle de même la direction et la courbure de la courbe près du point B.

On peut engendrer les points d'une telle courbe en utilisant le calcul barycentrique.

retour à la liste

Construire une bijection entre un ensemble A et un ensemble B consiste à mettre en correspondance parfaite les éléments de A avec ceux de B, ce qui n'est possible que si A et B ont, au sens intuitif, "autant d'éléments l'un que l'autre".

Exemple. Supposons que lors d'une fête, filles et garçons dansent en même temps par couples (chaque couple étant formé d'une fille et d'un garçon) : une bijection se trouve ainsi réalisée entre l'ensemble des filles et l'ensemble des garçons.

Dire que deux ensembles finis ont le même nombre d'éléments, revient à dire qu'il existe une bijection entre ces ensembles. Lorsque que deux ensembles infinis peuvent être mis en bijection, on dit qu'ils ont le même cardinal (on dit aussi qu'il ont la même puissance).

Les termes correspondance bijective, application bijective, ou bijection sont synonymes : de manière précise, une correspondance c d'un ensemble A vers un ensemble B est appelée une bijection de A sur B lorsque les couples (a,b) qui composent c satisfont aux deux propriétés suivantes :

(1) Tout élément a de A apparaît une fois et une seule comme premier terme dans un couple de c

(2) Tout élément b de B apparaît une fois et une seule comme second terme dans un couple de c.

1) signifie que c est une application de A (ensemble de départ) vers B (ensemble d'arrivée)
2) signifie que cette application c est à la fois surjective (tout élément de B apparaît au moins une fois) et injective (aucun élément de B n'apparaît deux fois ou plus).

retour à la liste

La formule du binôme de Newton donne le développement de (a+b)ⁿ, puissance n-ième du "binôme" a+b.

retour à la liste

Au sens courant, le mot bord traduit l'idée de bout, de frontière, de limite, de terminaison. Il s'applique à une étendue, à un morceau d'espace : le bord est formé des points qui ne sont ni dedans ni dehors.

En mathématiques, on emploi le mot bord pour :

- des surfaces planes : le bord d'un disque est un cercle, le bord d'une bande infinie est constitué de deux droites.
- des surfaces courbes : en soufflant doucement sur un anneau que l'on a plongé dans de l'eau savonneuse, on forme un bulbe liquide, une surface dont le bord est porté par l'anneau ; en soufflant plus fort on obtient une surface sans bord, une bulle.
- des volumes dans l'espace (lorsque qu'on peint un cube, on couvre son bord, c'est à dire la surface constituée de toutes ses faces).

La définition précise de bord dépend de la manière dont ces surfaces ou ces volumes sont étudiés.

Plus généralement, on peut parler de bord pour un ensemble de points dans un espace géométrique, pourvu que cet ensemble possède de "bonnes propriétés". Ainsi, pour un ensemble convexe (voir ce mot), la notion de bord est facile à définir. Elle coincide avec la notion de frontière, pourvu que l'ensemble convexe considéré ait la même dimension que l'espace géométrique dans lequel il apparaît.

retour à la liste

Ensemble d'étendue limitée, qui ne contient pas de points "infiniment loin".

Dans un espace métrique (où l'on dispose d'une notion de distance), un ensemble de points est dit borné s'il peut être inclus dans une boule. Autrement dit, un ensemble A de points est borné s'il existe un point O et un nombre r tels que : pour tout point M de A, la distance entre O et M ne dépasse pas r.

retour à la liste

Le cardinal d'un ensemble  E, aussi appelé sa cardinalité, ou représente, intuitivement, son nombre d'éléments, on le note card( E). Les cardinaux d'ensembles sont appelés les nombres cardinaux ou cardinaux.

• Le mot "cardinal" s'emploie pour les ensembles infinis comme pour les ensembles finis. Les cardinaux des ensembles finis sont les nombres entiers naturels.
• Comme les entiers naturels, les cardinaux des ensembles peuvent être comparés, additionnés ou multipliés entre eux, c'est pourquoi ils sont appelés les nombres cardinaux (ou cardinaux)
  
  • Par définition, deux ensembles A et B ont même cardinal s'il existe une bijection de A sur B. On dit aussi que ces ensembles sont équipotents.
  • Par définition, le cardinal d'un ensemble A est inférieur ou égal au cardinal d'un ensemble B, et on écrit card(A) card(B) si il existe une injection de A dans B.
  • Par définition, si deux ensembles A et B sont disjoints, on dit que le cardinal de l'ensemble AB (réunion de A et B)  est la somme des cardinaux des ensembles A et B et on écrit :
    card(AB)= card(A) + card(B)

  • Par définition, on dit que le cardinal de l'ensemble AxB (produit cartésien de A et B)  est le produit des cardinaux des ensembles A et B et on écrit :
    card(AxB)= card(A) x card(B)

• D'un point de vue formel, le cardinal d'un ensemble E, noté card( E), ou E (ou parfois #E) est la classe formée de tous les ensembles équipotents à E.

retour à la liste

Polygone régulier à 4 cotés. Un carré est un rectangle particulier, un rectangle dont les 4 cotés sont égaux.

	Dans le plan, pour que quatre points différents A,B,C,D pris dans cet ordre, soient les sommets d'un carré, il faut et il suffit que AB = BC = CD = DA (4 cotés égaux) et que les segments [AB] et [BC] (deux cotés adjacents) soient perpendiculaires.
	Dans le plan ou l'espace, pour que quatre points différents A,B,C,D pris dans cet ordre, soient les sommets d'un carré, il faut et il suffit que les segments AC et BD (les diagonales) aient même milieu, même longueur et soient perpendiculaires.

retour à la liste

Si les cotés d'un carré (figure géométrique) sont portés par les lignes d'un quadrillage, le nombre de cases intérieures à ce carré est un carré parfait.

1. Un nombre entier est un carré parfait (en abrégé un carré) si il est le résultat de la multiplication d'un nombre entier par lui-même :

• 1849 = 43x43 et 49 = (-7)x(-7) sont des carrés parfaits.
• Les carrés parfaits sont, dans l'ordre, 0 =0x0, 1 =1x1, 4 =2x2, 9 =3x3, 16 =4x4, 25 =5x5, etc.

2. Un nombre X est le carré d'un nombre x si X = xxx ; un nombre est un carré si c'est le carré d'un nombre de même espèce, c'est à dire pris dans le même ensemble de nombres.

• Un nombre et son opposé ont même carré.
• Théorème. Pour qu'un nombre réel soit un carré il faut et il suffit qu'il soit positif ou nul. Un nombre réel positif ou nul, a, est le carré d'un unique nombre réel positif ou nul b. Ce nombre b est appelé la racine carrée de a. Le nombre a est également le carré du nombre -b.
• Théorème. Tout nombre complexe est le carré d'un autre nombre complexe (et aussi de son opposé).

retour à la liste

Le produit cartésien de deux ensembles, A et B, noté Ax B, est l'ensemble constitué de tous les couples (a, b) dont le premier terme, a, est un élément de A et le deuxième terme , b, est un élément de B.

Plus généralement, le produit cartésien de n ensembles   A₁ , A₂ , ... , A_n ,  noté A₁ x A₂ x ... x A_n  est l'ensemble constitué de tous les n-uplets ( a₁ , a₂ , ... , a_n ) dont le k-ème terme  a_k  est un élément de  A_k  , pour chaque entier k compris entre 1 et n.

Exemple. L'usage d'un repère permet d'assimiler le plan au produit cartésien x : chaque point M du plan est assimilé au couple (x_M,y_M) formé par les coordonnées de M dans le repère choisi.
Plus généralement, le produit cartésien xx ... x(avec n facteurs) permet de définir l'espace réel à n dimensions, noté ⁿ.

C'est Descartes qui introduisit cette manière d'associer des nombres à des points, d'où l'adjectif cartésien qui est resté en vigueur.

couple, n-uplet, repère cartésien, coordonnées

retour à la liste

Lorsqu'on veut parler de tous les objets vérifiant une propriété donnée, on utilise le mot classe, ou collection, ou famille ou ensemble. Le mot "classe" est un terme primitif de logique mathématique, plus général que celui d'ensemble : on l'utilise surtout lorsque les objets considérés sont déjà construits à partir d'autres objets plus simples [ou encore lorsque l'usage des mots "ensemble" ou "famille" est incompatible avec les axiomes de la théorie des ensembles]* : on parle ainsi de classes de polynômes, de classes de fonctions, de classes d'ensembles, etc.

retour à la liste

Ce mot du langage courant est utilisé lorsqu'on veut parler de tous les objets vérifiant une propriété donnée. Dans la pratique, le mot "collection" est couramment utilisé pour classe, famille ou ensemble (bien que ces mots aient des sens mathématiques différents).

retour à la liste

Concaténer deux mots c'est former un nouveau mot en écrivant le second mot directement à la suite du premier, sans mettre d'espace entre les deux. Peu importe si ces mots sont dans le dictionnaire ou non.

retour à la liste

Deux objets mathématiques sont dits confondus si ce sont les mêmes. Ce terme s'emploie plutôt en géométrie.
Deux objets géométriques coÏncident s'ils sont confondus.

En géométrie, deux objets (figures) peuvent être égaux sans être confondus.

retour à la liste

Conique ou section conique. courbe plane obtenue en coupant un cône circulaire par un plan : une section conique est formée de tous les points communs au cône et au plan.

Une conique est soit une ellipse (le cercle étant un cas particulier possible), soit une hyperbole, soit une parabole, soit enfin (dans les cas dit "dégénérés" où le plan passe par le sommet du cône) la figure formée par deux droites sécantes (qui peuvent même être confondues lorsque le plan est tangent au cône)

Les coniques peuvent aussi être caractérisées de façon algébrique : ce sont précisément les courbes (planes) du second degré.

retour à la liste

Phrase qui a une sens mathématique précis et qui exprime une opinion, sans que l'on sache encore si ce qui est énoncé est vrai ou non. L'énoncé peut se révéler par la suite vrai (= on en fournit une démonstration, et la conjecture devient théorème) ou faux (= on fournit la démonstration du contraire, qui devient théorème) ou "ni vrai ni faux" (on prouve l'impossibilité de démontrer l'affirmation et l'impossibilité de démontrer son contraire).

Une conjecture qui s'avère ni vraie ni fausse est dite indépendante des axiomes (ou logiquement indécidable) : son énoncé peut devenir un nouvel axiome ou un postulat (on l'adopte pour nouvelle vérité afin d'en étudier les conséquences). Sa négation peut, elle aussi, être prise comme postulat.

• Un exemple de ce type est fourni par le "postulat des parallèles" considéré par Euclide : " par un point pris hors d'une droite on peut mener une parallèle et une seule à cette droite ". Axiome pour Euclide, cet énoncé a longtemps été considéré comme une conjecture par de nombreux mathématiciens, qui pensaient pouvoir le démontrer à partir des autres axiomes d'Euclide, jusqu'à ce que Bolyai, Gauss et Lobachevski, au XIXème siècle, puis Beltrami, Klein et Poincaré prouvent, grâce à une construction "euclidienne" de géométries "non-euclidiennes", l'impossibilité de le démontrer (pourvu que les autres axiomes d'Euclide, n'entraînent eux-mêmes aucune contradiction). L'impossibilité de démontrer le contraire du postulat est aussi établie.

retour à la liste

On dit qu'un ensemble a la puissance du continu s'il peut être mis en bijection avec l'ensemble des points d'une droite réelle ou, ce qui revient au même avec l'ensemble des nombres réels.

dénombrable, cardinal, infini

retour à la liste

Intuitivement, une fonction f(x) est continue lorsqu'une petite erreur sur la valeur de x (variable) n'entraîne pas d'écart important sur la valeur de f(x) : si la variable x varie peu, l'image f(x) varie peu.

Imaginons la fonction f comme un procédé de fabrication du produit f(x) à partir de la matière première x, la fonction est continue si le procédé est fiable, c'est à dire s'il permet de garantir un résultat malgré de petites fluctuations de la matière première. Plus précisément, f est continue si elle a la propriété suivante: quelque soit la matière première a, si on tolère un écart e sur le produit voulu f(a), il existe alors une garantie a pour la matière première qui permet de satisfaire à coup sûr la demande : f(x) vaudra f(a) (à e près) dès que x vaudra a (à a près).

Mathématiquement, une fonction est continue si elle admet une limite en tout point où elle est définie (la valeur de cette limite coïncide alors, nécessairement, avec la valeur de la fonction au point considéré).

Illustration par un exemple. Imaginons que f soit la fonction qui envoie un cube sur une sphère de même centre (appelons le O) de la façon suivante : à un point M du cube on fait correspondre le point P = f(M) de la sphère qui est aligné avec M et O et qui est situé de l'autre côté que O par rapport à de M. Qu'un point Q soit proche de P peut dépendre de la taille de la sphère, et aussi de la finesse de la précision qu'on souhaite. Si la sphère est de la taille de la terre, et s'il s'agit de faire une passe au football, une précision de l'ordre de 1 cm n'est pas nécessaire, mais s'il s'agit d'une partie de golf, il vaut mieux ne pas rater le centre du trou à plus d'un centimètre ... Dans un cas comme dans l'autre, il y a un moment où on estimera que Q est proche de P et ce moment n'est pas toujours le même suivant les applications numériques. Notre fonction est continue parce que peu importe la précision voulue autour de P sur la sphère, on trouvera toujours une petite région autour de M sur le cube dans laquelle chaque point N aura une image Q = f (N) "proche" de P. Et si notre fonction part d'un cube beaucoup plus petit, ou beaucoup plus gros, il n'y aura qu'à réduire ou agrandir en conséquence la taille de la région "proche" de M. Notre fonction sera toujours continue.

Remarque 1. La Topologie* permet de définir la continuité très simplement à partir de la notion d'ensemble ouvert.

Soit f une fonction d'un espace topologique E dans un espace topologique F. La fonction f est continue si, pour tout ensemble ouvert W de F (l'espace d'arrivée), les points p de E (l'espace de départ) dont l'image f(p) est dans W forment un ensemble ouvert (de E).

Plus localement, la fonction f est continue en un point p de son domaine de définition D_f si on a la propriété suivante :

(" W ouvert contenant f(p)) ($ V ouvert contenant p) [(xV et xD_f)f(x)W)]

ou sous une forme équivalente :

(" W voisinage de f(p)) ($ V voisinage de p) (f(VD_f)W)

Remarque 2. [* L'Analyse Non Standard permet de donner une définition à la fois intuitive et rigoureuse de la continuité : une fonction numérique est continue si les images de deux nombres "infinitésimalement proches" sont également "infinitésimalement proches" *].

retour à la liste

retour à la liste

syn. suite convergente.

retour à la liste

On dit qu'une suite ( s_n) est convergente si elle admet une limite lorsque n tend vers +. Si L est une telle limite, on dit que la suite converge vers L.

retour à la liste

En géométrie, un ensemble convexe est un ensemble de points qui contient tous les segments joignant deux de ses points.

Un corps convexe est un ensemble convexe qui n'est pas dégénéré, c'est à dire qui a la même dimension que l'espace ambiant.

retour à la liste

Voir barycentre.

retour à la liste

Une correspondance d'un ensemble A vers un ensemble B est la donnée de A, de B, et d'un ensemble C de couples de la forme ( a, b) où aA et où b B. Autrement dit C est une partie quelconque du produit cartésien Ax B, appelée le graphe de la correspondance (A,B,C).

graphe, relation binaire

retour à la liste

Deux droites se coupent si elles ont au moins un point commun : elles sont sécantes ou confondues.

Plus généralement, deux figures géométriques se coupent si elles ont au moins un point en commun.

Deux ensembles se coupent s'ils ont au moins un élément commun, autrement dit si leur intersection n'est pas vide.

retour à la liste

Liste de deux éléments, dans un ordre précis. Le couple formé des éléments a et b est noté (a,b),. On a (a,b)(b,a) sauf si a=b.

Avec les éléments d'un ensemble à  n éléments on peut former  nx n couples différents.

• La notion de couple est une notion primitive de la théorie des ensembles. Elle permet de définir le produit cartésien de deux ensembles.
• Un couple de nombres écrits en chiffres ou un couple de coordonnées se notera sous la forme (a;b).

  produit cartésien, paire, n-uplet

retour à la liste

Ligne que l'on peut parcourir pour aller d'un point à un autre. Le mot "courbe" est utilisé dans de nombreuses situations avec des sens variables. Dans son usage courant, il traduit l'idée de ligne d'un seul tenant et sans épaisseur (courbe dite unicursale), pouvant être parcouru sans lever le crayon" (courbe dite traçable); que cette ligne soit vraiment sinueuse ou non, peu importe, on l'appelera courbe : une courbe est donc un parcours, un trajet, un itinéraire... On parle de courbe fermée lorsque le point de départ et le point d'arrivée de la courbe sont les mêmes, sinon on parle simplement de courbe ou d'arc de courbe.

1.Définition courante (courbe unicursale ou arc de courbe): une courbe (ou un arc de courbe) dans un espace E (le plan, l'espace, etc.) est une application continue d'un intervalle I de dans E :

C :  tIC( t)E

A chaque valeur de la variable t, prise dans l'intervalle I de, correspond ainsi un point C( t). Pour I=[0,1] par exemple, on peut penser à la trajectoire d'un point mobile qui se trouve à l'instant t=0 à la position C(0) et arrive à la position C(1) à l'instant t=1 : la position à l'instant t est le point C(t). La courbe est dite fermée si C(1)= C(0). Si on restreint la variable t à évoluer dans un intervalle [ a,b] inclus dans I, on obtient une courbe

C' :  t[ a,b]C'( t)E

où C'( t)est définie par C'( t)=C( t). On dit que C' est l' arc de la courbe C compris entre  C( a) et  C( b). Les points C( a) et  C( b) sont les extrémités de C'.

Chaque point de la forme C( t) est appelé un point de (ou sur) la courbe C. Des points distincts M₁, M₂, Š,M_n de C sont dit dans l'ordre si ils correspondent à des valeurs croissantes de la variable t : M₁= C ( t₁),  M₂= C ( t₂) ,Š, M_n= C ( t_n) avec  t₁< t₂<Š< t_n .
Cette idée sert notamment à définir la longueur d'une courbe ou d'un arc de courbe.

• On donne aussi le nom de courbe à l'ensemble C(I) de tous les points de la courbe. Ce point de vue implique qu'une même courbe puisse être définie de plusieurs manières.

Une manière courante de définir une courbe est d'en donner une équation

Par exemple, si O est un point donné du plan et si M est une variable qui désigne un point (variable) du plan, on peut voir l'expression OM=3 comme une équation qui définit le cercle de rayon 3 et de centre O.

On se sert souvent d'équation où les variables représentent des coordonnées. L'équation est vérifiée par les cordonnées d'un point ssi ce point est sur la courbe. (voir définition générale et courbes algébriques)

Si O est l'origine d'un repère orthonormé du plan, une équation du cercle de rayon 3 et de centre O. est  x²+ y²=9. Ici, les variables x et y sont les coordonnées d'un point (variable) du plan.

Courbes paramétrées. Une courbe C(t) est dite paramétrée lorsque les coordonnées de ses points sont définies par des formules, (ces définitions sont alors les équations paramétriques de la courbe). Ainsi, un système d'équations paramétriques pour le cercle de rayon 3 et de centre O, dans un repère orthonormé d'origine O est :

x( t) = cos t	pour t[ 0 ;  2]
y( t) = sin t

Courbes traçables. En fait certaines courbes sont tellement bizarres qu'on ne peut pas les tracer en pratique. Peano et Hilbert, par exemple, ont construit des courbes qui remplissent totalement l'intérieur d'un carré! La possibilité concrète de représenter une courbe C par un tracé exige plus que la continuité de l'application C : la courbe doit posséder une tangente en tout point (sauf, peut-être en des points exceptionnels qui seront en nombre fini : de telles courbes sont dites de classe C₁ par morceaux*) et avoir une longueur bornée (ces courbes sont dites rectifiables*).

2. Définition plus générale. On peut généraliser la définition courante en appelant courbe dans un espace E (le plan, l'espace, etc.) une application continue d'une partie P de dans E [ avec une définition généralisée de la continuité]*. Dans le cas où P est une réunion d'intervalles, on obtient ainsi des courbes formée de plusieurs morceaux, chaque morceau étant une "courbe" (unicursales) au sens de la définition courante. Les courbes définies par une équation sont souvent de ce type (voir courbes algébriques).

Courbes algébriques. Elles représentent dans un espace donné (le plan, l'espace, etc.) l'ensemble des solutions d'équations algébriques. Ces courbes sont "générales" en ce sens qu'elle sont généralement formées de plusieurs "morceaux" (voir courbes générales). Lorsque les équations utilisées sont de degré d ou moins, les courbes correspondantes sont dites de degré d.

Dans le plan l'ensemble des points dont les deux coordonnées vérifient une équation algébrique à deux variables est appelé une courbe algébrique. En prenant , par exemple, une équation du second degré, on obtient une conique. Avec une équation du troisième (resp. quatrième) degré on obtient une cubique (resp. une quartique).

Dans l'espace, une seule équation définit en général une surface ; il faut donc un système de deux équations pour définir une courbe algébrique dans l'espace, qui apparaît ainsi comme la partie commune à deux surfaces. On retrouve par exemple les coniques en coupant un cone par un plan.

géodésique, longueur*, tangente*, arc ou courbe de Jordan*.

retour à la liste

Le système décimal est le moyen usuel d'écrire les nombres (entiers, fractionnaires ou réels). Il utilise les dix chiffres arabes

la virgule ",", les signes " + " et"-" et le symbole "..." .

Le principe de ce système est la numération de position, ce qui signifie que chaque chiffre indique une quantité qui dépend de la position du chiffre dans l'écriture.

Une écriture décimale se compose, dans l'ordre, d'un signe (+ ou - , le signe + étant souvent omis) d'une liste de chiffres, éventellement suivie par une virgule (",") et par d'autres chiffres et se terminant éventuellement par trois points (symbole "...").

Exemples : chacune des écritures suivantes :

1789
-1,5 
1,4142
1,4142...
-3,1415...
5,00000...
4,99999... 
0,12346789101112131415...

est une écriture décimale.

Les trois points indiquent que la suite des chiffres doit être prolongée par la pensée au delà de ce qui est écrit, en suivant des règles qu'il faut préciser si elles ne sautent pas aux yeux : 1,414... peut se prolonger aussi bien 1,414141414... (répétition des chiffres 1 et 4, obtenue en poursuivant la division de 140 par 99) qu'en 1,41421356237309... (développement décimal de la racine carrée de 2)

Dans l'écriture décimale d'un nombre x, on place son signe (+ ou -) à gauche (dans la pratique courante, on omet le signe +) . On n'utilise la virgule ( , ) que si x n'est pas entier.

- les chiffres placés à gauche de la virgule (tous les chiffres si x est entier) forment la partie entière du nombre x. Le chiffre placé juste à gauche de la virgule (ou le dernier chiffre, si x est entier) indique un nombre d'unités. Vers la gauche, les chiffres suivants correspondent dans l'ordre, aux nombres de dizaines, de centaines, de milliers etc. (puissances positives successives du nombre 10) qui contribuent à la quantité x. :

Exemple : 1789 = 1 x10³+ 7 x10²+ 8 x10 + 9 x1

-Les chiffres placés à droite de la virgule, appelés les décimales du nombre x, sont utilisés pour les nombres non entiers. Ils constituent le développement décimal du nombre x : le chiffre immédiatement à droite de la virgule indique le nombre de dixièmes d'unités. Plus à droite, les chiffres correspondent successivement aux nombres de centièmes, de millièmes, de dix-millièmes etc., c'est à dire comptent les puissances négatives du nombre 10 qui contribuent à la quantité x.

Exemple : 1234,0123 est écriture du nombre égal à la somme

1 millier + 2 centaines + 3 dizaines + 4 unités + 0 dixièmes + 1 centièmes + 2 millièmes +3 dix-millièmes

Le développement décimal d'un nombre réel est par principe unique et comporte une infinité de décimales. Comme on ne peut les écrire toutes, on ne marque que la ou les premières (le dernier chiffre indiquant la précision avec laquelle le nombre est écrit) puis on place trois points ("... "), pour indiquer que le développement se pousuit.

Ex. L'écriture décimale, avec 4 décimales, deest 1,4142...

Par convention, l'écriture décimale d'un unique nombre réel Si toutes les décimales le nombre réel x sont nulles à partir d'un certain rang, on dit que est un nombre décimal. On n'écrit alors que les décimales qui précèdent l'infinité de 0.

Exemples : -5  ,     -5,00000...   ,    -4,99999...

sont des écritures décimales différentes de l'entier relatif - 5.

Attention ! 4,99999... est aussi une écriture décimale correcte de tout nombre réel qui est compris entre le nombre entier décimal 4,99999 et l'entier 5.

retour à la liste

Les nombres décimaux sont ceux qui s'écrivent de manière finie en base 10. Ce sont les "nombres à virgule" utilisé dès l'école primaire et dans la vie courante. Ils sont obtenus en divisant un nombre entier par 1, 10, 100, 1000, 10 000, etc., autrement dit par une puissance de 10. Voir système décimal.

Les nombre décimaux sont précisément les nombres réels qui admettent deux écritures décimales distinctes équivalentes, l'une (dite propre) se terminant par une infinité de 0, l'autre (impropre) par une infinité de 9.

retour à la liste

Manière de faire comprendre l'usage d'un mot et la "chose" à laquelle ce mot correspond. Les définitions courantes, celles qui se trouvent dans les dictionnaires ont pour but d'indiquer les différents significations possibles d'un mot. Les définitions mathématiques ont pour but de préciser comment le mot doit être employé lorsqu'on fait des mathématiques.

Ce sont les définitions mathématiques qui donnent naissance aux "êtres mathématiques" et permettent de prouver leurs propriétés (théorèmes).

Une définition mathématique introduit à la fois un mot et un objet auquel ce mot est lié, formant ainsi une notion mathématique (attachée à un domaine particulier) ou un concept mathématique (relié à plusieurs domaines). Pour être correcte, une définition doit indiquer son contexte, c'est à dire le domaine mathématique où la notion a un sens (elle y est étudiée comme objet ou elle sert d'outil pour étudier d'autres objets): l'usage du mot correspondant dans ce domaine est alors fixé une fois pour toute, le mot défini devient un mot "réservé" pour son emploi mathématique.

Le plus souvent une même notion mathématique reçoit plusieurs définitions mathématiques dont on prouve qu'elles sont équivalentes, c'est à dire qu'elles correspondent au même objet mathématique.

Le rôle d'une définition courante, "intuitive" (et donc extra-mathématique) pour un objet mathématique est d'expliquer sa (ou ses) définitions mathématiques, en montrant à l'aide d'images, de comparaison, de représentations variées. les situations où cet objet est intéressant.

démonstration

retour à la liste

Seul moyen admis par les mathématiciens pour dire que quelque chose est vrai. En mathématiques, pour qu'un énoncé soit tenu pour certain, il doit être démontré, c'est à dire faire l'objet d'une démonstration (mathématique). Une propriété démontrée prend le nom de théorème. La Logique est la partie des mathématiques qui précise et étudie les règles auxquelles obéissent les démonstrations.

Au sens courant, "démonstration" est synonyme de preuve mathématique : il s'agit d'un raisonnement qui, par un enchaînement logique obéissant à un ordre rigoureux, aboutit à une conclusion à partir d'une hypothèse.

• Une preuve mathématique comprend trois types d'ingrédrients
  
  • Des hypothèses H₁, H₂, H₃,... , c'est à dire des énoncés supposés vrais.
  • Des raisonnements (ou déductions) R₁, R₂, R₃, ... c'est à dire des énoncés qui s'enchainent logiquement (suivant les règles fournies par la Logique).
  • Des conclusions (ou thèses) C₁,C₂,C₃,... c'est à dire des énoncés terminaux auxquels aboutissent les raisonnements.

  On résume une preuve mathématique par un énoncé unique :

  Si les hypothèses H1, H2, H3,... sont vraies, alors les conclusions C1,C2,C3,... sont vraies.

Cet énoncé est l'énoncé du théorème qui est prouvé par l'ensemble de la preuve.

Démonstrations formelles. Au sens de la pure logique, c'est à dire au sens formel, on peut toujours présenter une démonstration comme une succession d'énoncés tous vrais. Chacun de ces énoncés présenté est

soit (a) une hypothèse : un axiome (hypothèse générale prise comme point de départ de nombreux raisonnements de même type), une définition (hypothèse qui introduit un mot ou un symbole nouveau en précisant comment il sera utilisée par la suite) ou une donnée (hypothèse particulière qui précise la situation que l'on souhaite étudier)
soit (b) une conséquence logique d'un ou de plusieurs énoncés précédent.

L'énoncé qui arrive en dernier dans un telle succession est le théorème démontré par cette succession d'énoncés. (On remarque que si on choisi un énoncé particulier E dans une démonstration formelle et si on supprime les énoncés qui y apparaissent après l'énoncé E, on obtient encore une démonstration formelle : ainsi, au sens strict, chaque énoncé E d'une démonstration formelle est un théorème !)

Les démonstrations formelles, même pour les choses les plus simples, sont épouvantablement longues. Dans la pratique, lorsqu'on rédige une démonstration, on se limite à indiquer ce qui est vraiment nouveau et on demande au lecteur de vérifier qu'il peut combler les "trous". On ne répète ni les démonstrations déjà faites, ni les hypothèses ou définitions qui sont évidentes d'après le contexte ; on se borne à donner les étapes principales du raisonnement en précisant pour chaque énoncé, et en expliquant au besoin, son statut logique :

- hypothèse,
- théorème démontré auparavant,
- ou conséquence d'autres énoncés précédemment écrits.

Exemple : 2 + 2 = 4 est un théorème, conséquence logique de la notion primitive de successeur (un des axiomes des nombres entiers naturels, qui introduit la notation a⁺ pour désigner le successeur d'un entier naturel a), de l'existence et de la définition de l' addition (qui est construite à partir des axiomes des entiers naturels), de la définition de 2 (comme successeur de 1, lui même successeur de 0) et de la définition de 4 (comme successeur du successeur de 2).

Comme rédaction d'une démonstration de ce théorème, on peut proposer :

2+2 = 2+(1⁺)  par la définition de 2
2+(1⁺)=(2+1)⁺  par la définition de l'addition
                  (en effet, par définition, une somme de la forme a+(b⁺) est égale à (a+b)⁺.
(2+1)⁺ = (2+0⁺ )⁺  par la définition de 1
(2+0⁺ )⁺ = ((2+0)⁺ )⁺   par la définition de l'addition (comme ci-dessus)
((2+0)⁺ )⁺ = (2⁺ )⁺   par la définition de l'addition
                  ( en effet, par définition, une somme de la forme a+0 vaut a ).
(2⁺ )⁺ =4   : c'est la définition de 4
De toutes les égalités précédentes on déduit 2+2 = 4.

retour à la liste

Un ensemble est dit dénombrable si on peut numéroter ses éléments. Plus précisément, un ensemble est dénombrable s'il peut être mis en bijection avec une partie de l'ensemble des entiers naturels.

Un ensemble infini est dénombrable ssi il peut être mis en bijection avectout entier.

On démontre que l'ensemble des nombres rationnels est dénombrable.

[Cantor] L'ensemble des nombres réels n'est pas dénombrable.

retour à la liste

Un ensemble A est dense dans un ensemble B si A est inclus dans B et si chaque élément de B peut être approché indéfiniment (aussi près qu'on veut) par des éléments de A.

Précisément :

• Si une distance d a été définie sur B, A est dense dans B si

" pour tout bB, pour tout e > 0 ( e est l'erreur tolérée), il existe aA tel que d(a, b) < e ".

• Si l'ensemble B est ordonné et contient A, A est dense dans B si

Ainsi, l'ensemble des nombres décimaux est dense dans l'ensemble des nombres rationnels (ordonné avec la relationusuelle); l'ensemble des nombres rationnels est dense dans l'ensemble des nombres réels (ordonné avec la relationusuelle) .

retour à la liste

retour à la liste

La dérivée selon Newton : "Le quotient ultime de deux accroissements évanescents"...

retour à la liste

La différence de deux éléments a et b est, s'il existe, l'élément qu'il faut ajouter à b pour obtenir a.

Dire que « d est la différence de a et b » équivaut donc à dire « a = b+d »

Lorsqu'elle existe la différence des éléments a et b se note a-b.

Le mot différence ne s'emploie que lorsqu'une addition a été définie, et lorsque les propriétés de cette addition garantissent que la différence de deux éléments existe et est unique.

retour à la liste

Cet adjectif vient du nom du mathématicien grec Diophante (vivant à Alexandrie au IVème siècle) ; il indique que ce dont on parle ne fait intervenir que des nombres entiers.

Une  équation diophantienne est une équation (généralement polynomiale) dont les inconnues sont des nombres entiers (positifs ou non).

La plus célèbre de ces équations est l'objet du "théorème" de Fermat : Xⁿ + Y ⁿ = Z ⁿ.

Un théorème de logique très profond, dû à Matjasevic, montre que tout ensemble de nombres entiers dont les éléments peuvent être construits un par un au moyen d'un algorithme coïncide avec l'ensemble des solutions d'une équation diophantienne.

L'ensemble des nombres premiers a cette propriété, puisque la qualité pour un nombre d'être premier est reconnaissable au moyen d'un algorithme.

retour à la liste

Nombre qui exprime que deux choses sont éloignées, écartées, différentes...

Intuitivement, on sait bien que la distance d'un endroit à un autre n'est pas la même " par la route " ou " à vol d'oiseau ", qu'elle peut se mesurer en " dix minutes à pied " ou " une heure d'avion " ou en " stations de métro ". Une copie peut être " plus ou moins ressemblante " à un original.

Une distance d est une fonction (numérique) qui s'applique à deux objets de même nature (deux points, deux nombres, deux polynômes, deux figures, etc) et pour laquelle les propriétés :

• d(A, B) = 0 ssi A = B
• d(A, B) = d(B, A)
• d(A, B)d(A, C) + d(C, B) (inégalité triangulaire)

doivent être vérifiées pour tous les choix possibles des objets A, B, C.

La distance habituelle (distance euclidienne) est définie à l'aide des axiomes de la géométrie euclidienne* ; elle vérifie la propriété fondamentale :

(ceci est vraie dans tous les espaces euclidiens, droite, plan, espace, etc.). Le calcul des distances euclidiennes est facilité par le théorème de Pythagore*.

Mais il y a d'autres distances :

• une distance purement qualitative, où deux objets différents sont toujours à la distance 1 l'un de l'autre ;
• une distance entre les branches d'un chêne qui compte le nombre d'embranchements qu'il faut franchir pour aller de l'une à l'autre (valable pour n'importe quel arbre, même ... généalogique) ;
• le temps le plus court pour aller en voiture d'un point de Paris à un autre ne définit pas une distance (à cause des sens uniques et des feux tricolores) sauf pour les chauffards, car l'aller et le retour ne se feront pas toujours dans le même temps : d(A, B)d(B, A) dans certains cas.
• la distance " SNCF " (mesurée en km parcourus): si on ne tient pas compte des petites lignes "transversales" qui n'ont pas encore été fermées, on va d'une ville à une autre en passant par Paris, sauf si les deux villes sont sur une même ligne au départ de Paris, auquel cas on va de l'une à l'autre directement, sur cette ligne.
• etc, etc.

retour à la liste

Deux objets géométriques sont distincts si ils ne sont pas confondus : il y a au moins un point de l'un qui n'appartient pas à l'autre.

Deux figures géométriques distinctes peuvent être égales.

retour à la liste

Le nombre 3 divise 2001 car 2001 = 3x667. Par contre, 3 ne divise ni 2000 ni 2002 : aucun nombre entier ne peut donner 2000 ou 2002 lorsqu'on le multiplie par 3.

Notation. On écrit ba pour signifier que b divise a et ba  pour signifier que b ne divise pas a :       32001 ,   315    ,   32002

Dans un ensemble où l'on dispose d'une multiplication qui est commutative, notée x, on dit qu'un élément b divise un élément a, lorsque qu'il existe un élément q tel que a soit égal au produit b x q. On dit aussi que le nombre b est un diviseur de a ou que a est divisible par b, ou encore que a est multiple de b.

Remarque. Lorsque a est le produit de plusieurs facteurs, chacun de ces facteurs divise a.

On emploie surtout ces mots dans les cas où la division est problématique c'est à dire lorsque la division par un élément non nul n'est pas toujours possible (tel est le cas pour les nombres entiers, les classes de congruences*, les polynômes, les matrices*).

retour à la liste

Si un nombre N est le produit de plusieurs autres nombres, chacun de ces nombres est appelé un diviseur de N.

Tout nombre entier naturel N peut s'écrire 1xN ; les entiers 1 et N sont des diviseurs de N appelés diviseurs impropres. Les autres diviseurs éventuels de N sont appelé ses diviseurs propres. Les nombres entiers autres que 1 qui n'ont pas de diviseur propre sont appelés les nombres premiers.

Remarque. Avec la multiplication usuelle des nombres entiers, rationnels, réels, ou complexes, un produit de facteurs non nul n'est jamais nul. Mais pour d'autres types de nombres ou pour d'autres multiplications, il peut arriver que le produit de deux nombres non nuls soit nul, c'est à dire égal à 0, l'élément neutre de l'addition. Dans un tel produit, chacun des facteurs est appelé un diviseur de zéro.

retour à la liste

Opération "inverse" d'une multiplication, ou calcul qui permet d'effectuer une telle opération.

1. Étant donné un nombre A et un nombre B, on cherche un nombre Q tel que A soit égal à BxQ. Ce nombre Q , s'il existe et est unique, est appelé le quotient de A par B (ou quotient exact de A par B) et est noté ou A/B (ou aussi A: B ou encore A B ). On appelle division l'opération qui aux deux nombres A et B, pris dans cet ordre, fait correspondre le quotient A/B . Lorsque le nombre B a un inverse B' =la division de A par B revient à la multiplication de A par B', autrement dit on a : = A x.

La division est possible (le quotient existe) pour les nombres décimaux, rationnels, réels ou complexes, pourvu que B soit différent de 0. Pour les nombres entiers, le quotient exact n'existe que si A est un multiple de B, mais on peut faire une division approchée, qui fait apparaître un "reste", c'est la division euclidienne .

2. On appelle aussi division tout procédé de calcul qui permet d'obtenir le résultat d'une division. Par exemple, la division que l'on apprend à l'école primaire permet de calculer le quotient entier d'un nombre entier positif A par un autre nombre entier positif B, avec un reste lorsque la division "ne tombe pas juste", c'est à dire lorsque A n'est pas un multiple de B. Voir division euclidienne .

division euclidienne

retour à la liste

Lorsque la division d'un nombre entier positif A par un autre nombre entier positif B n'est pas possible, c'est à dire si A n'est pas un multiple de B, on s'intéresse au plus grand multiple de B, qui est inférieur ou égal à A. Ce multiple s'écrit BxQ et le nombre A s'obtient alors en ajoutant à BxQ  un nombre entier positif R :

Le nombre Q est appelé le quotient entier de A par B, tandis que le nombre R est appelé le reste de la division de A par B. L'opération qui consiste à associer aux nombres A et B, pris dans cet ordre, les nombres Q et R est appelé la division euclidienne.

Remarque. Le reste R de la division euclidienne de A par B est nécessairement inférieur à B. En effet, par définition du nombre BxQ, tous les multiples de B supérieurs à BxQ sont supérieurs à A ; en particulier le nombre BxQ +B, égal à Bx(Q+1) est supérieur à A c'est à dire à BxQ + R. D'où B supérieur à R. On a le théorème plus précis suivant.

(de la division euclidienne)

Si A et B sont des nombres entiers positifs , le quotient entier de A par B et le reste de la division euclidienne de A par B sont les seuls entiers Q et R positifs ou nuls qui vérifient :

A = BxQ + R avec 0R<B

• Ce qui précède s'applique sans changement pour un entier A de signe quelconque, ( B étant, lui, positif).
• Le principe de la division euclidienne se généralise facilement aux nombres décimaux et aussi aux polynômes.

retour à la liste

On dit que deux choses sont égales si l'une peut remplacer l'autre en toute situation. Deux objets égaux, A et B, doivent être considérés comme identiques : bien que de noms différents, ils constituent une seule et même entité.

Dans la pratique, il arrive souvent que dans un cadre particulier (la géométrie, l'algèbre, la théorie des graphes théorie particulière) deux objets différents jouissent exactement des mêmes propriétés ou jouent le même rôle dans les raisonnements. On convient alors de dire de ces objets qu'ils sont égaux.

• Ainsi, en géométrie métrique, deux figures que l'on peut faire coïncider exactement au moyen d'une isométrie (une transformation qui conserve les distances) seront dites égales. En particulier deux segments sont égaux s'il ont même longueur . Des figures égales possèdent les mêmes propriétés.

retour à la liste

Ce mot exprime l'idée de tas, de collection, de famille : on s'en sert chaque fois que l'on réunit plusieurs choses, par la pensée ou dans la pratique. On peut s'intéresser à un sac de billes, à un jeu de cartes, à une boite d'allumettes, à un répertoire téléphonique, un panier de fruits, un groupe de personnes, les voitures rouges que jai vu dans la rue, etc.

Il y a deux manières courantes de définir un ensemble d'objet:

• en faisant une liste (on dit alors que l'ensemble est défini "en extension")
• en énonçant les propriétés que doivent posséder les objets que l'on réuni. (l'ensemble est alors défini "en compréhension")

Le mot ensemble est une notion primitive des mathématiques : on l'introduit en même temps que les mots "élément" et "appartient à" à l'aide des axiomes de la théorie des ensembles*.

Dans la pratique mathématique courante, on utilise indifféremment, les mots ensemble, classe, collection, ou famille.

retour à la liste

retour à la liste

Abréviation pour " nombre entier relatif ". Les nombres entiers relatifs sont "les nombres entiers avec signe" ; ils généralisent les nombres entiers naturels.

+ 5,    - 4 ,   - 1,   + 4,   - 654 ,   + 2005 sont des entiers relatifs.

On décide que +0 et -0 sont un seul et même nombre entier relatif, nombre que l'on note simplement 0. On dit que 0 n'a pas de signe ou encore que 0 est de signe nul.

On se sert des nombres entiers relatifs pour mesurer des grandeurs dans deux directions opposés. Un nombre entier relatif est soit nul soit positif soit négatif, suivant que c'est 0, qu'il commence par le signe + ou par le signe -.

Exemples :

Un thermomètre indique des températures négatives (au dessous de zéro) ou positives (au dessus de zéro).
Le bilan d'une entreprise sera positif s'il elle a gagné de l'argent, négatif si elle en a perdu.
L'année -654 se situe 654 ans avant l'origine choisie par le calendrier.

Une graduation avec des entiers relatifs permet de se repérer. Le nombre 0 est choisi comme origine.

Une graduation de la droite horizontale place généralement les entiers positifs à droite de 0 et les entiers négatifs à gauche.	Dans une graduation verticale, les positifs sont placés au dessus de 0, les entiers négatifs au dessous.

Notation des nombres entiers relatifs. Le nombre 0 mis à part, l'écriture d'un nombre entier relatif se compose d'un signe et d'un nombre entier naturel, appelé sa valeur absolue. :

5 est la valeur absolue de - 5, 3 est la valeur absolue de +3.
+2005 et -2005 ont chacun pour valeur absolue 2005.

Les nombres entiers relatifs généralisent les nombres entiers naturels, ce qui explique qu'en pratique on n'écrive pas les signes + des nombres relatifs positifs : on confond l'entier relatif +3 avec l'entier naturel 3.

L'ensemble des entiers relatifs se note (initiale du mot "nombre" en allemand).

Addition des nombres entiers relatifs. Les nombres relatifs peuvent être utilisés pour indiquer des déplacements sur une graduation : le nombre +3 indique un déplacement de 3 graduations vers la droite, le nombre -5 un déplacement de 5 graduations vers la gauche. C'est ce point de vue qui permet le mieux de comprendre l'addition de deux nombres entiers relatifs : additionner deux nombres revient à combiner les déplacements qu'ils représentent.

Par exemple pour additionner -5 et +3, on se déplace de 5 graduations vers la gauche (signe -) puis de 3 graduations vers la droite (signe +) : on se retrouve alors à 2 graduations du point de départ, vers la gauche : le déplacement total est celui qu'on aurait obtenu avec le même point de départ et le nombre -2. En résumé, -5 et +3 ont pour somme le nombre  - 2.

Il est évidemment plus commode pour calculer une somme de prendre comme point de départ le point marqué 0, Ainsi, après avoir effectué les déplacements indiqués par les nombres relatifs que l'on veut additonner, on lit en face du point d'arrivée le nombre correspondant à la somme voulue.

On démontre que l'opération addition a les propriétés suivantes

• commutativité : quel que soit les entiers A et B on a A+B=B+A.
• associativité : quel que soit les entiers A, B, C on a (A+B)+C = A+(B+C)
• Existence d'un élément neutre, 0 : quel que soit l'entier A on a 0 + A = A + 0 = A
  Existence d'un opposé : quel que soit l'entier A, il en existe un autre A' telque A+A'=A'+A=0. L'opposé d'un entier relatif s'obtient en gardant sa valeur absolue et en changeant son signe. Ainsi -3 est l'opposé de 3 (notation simplifiée de +3) et 3 est l'opposé de -3.

notation pour les opposés :

Par convention l'opposé d'un entier relatif A se note opp(A) ou plus simplement -A.

opp(-3) = -(-3) = +3 = 3 = et opp (3) = -3 = opp(+3) = -(+3)

De plus si opp(A) intervient comme terme d'un somme, par exemple dans une expression de la forme B+opp(A)+.C ou B+(-A) + C, on simplifiera l'écriture en placant le seul signe - devant A :

B+opp(A)+.C ou B+(-A) + C deviennent B-A+C.

On remarque que dans de telles expressions, le signe "moins" doit être interprété comme "j'ajoute l'opposé de".

Cet emploi du signe - reflète la soustraction des nombres naturels

5-3 (au sens de la soustraction d'entiers naturels) vaut 2
5-3 (au sens d'addition d'entiers relatifs) vaut (+5)+(-3) soit (+2) soit 2.

mais il la généralise :

la soustraction 3-5 entre entiers naturels est impossible
alors que 3-5 , au sens des entiers relatifs vaut (+3)+(-5) soit (-2)

Multiplication des nombres entiers relatifs. Elle s'obtient en généralisant la multiplication des nombres entiers naturels de manière à préserver ses propriétés habituelles

• commutativité : quel que soit les entiers A et B on a AxB=BxA.
• associativité : quel que soit les entiers A, B, C on a (AxB)xC = Ax(BxC)
• Existence d'un élément neutre, 1 : quel que soit l'entier A on a 1xA = Ax1 = 1
• distributivité par rapport à l'addition : quel que soit les entiers A, B, C on a Ax(B+C) = (AxB)+(AxC)

On peut définir la multiplication de deux entiers relatif par les 4 règles suivantes, qui couvrent tous les cas :

le produit d'un entier positif A par un entier positif B est le produit AxB des entiers naturels A et B
(-A)xB = - (AxB) : le produit d'un entier négatif -A par un entier positif B est l'opposé du produit AxB.
Ax(-B) = - (AxB) : le produit d'un entier positif A par un entier négatif -B est l'opposé du produit AxB.
(-A)x(-B) = AxB : le produit d'un entier négatif -A par un entier négatif -B est le produit AxB.

En résumé on a la règle des signes suivante : on obtient le produit XxY des deux entiers relatifs X et Y en faisant le produit de leur valeurs absolues et en affectant ce produit du signe  +  lorsque X et Y sont de même signe, ou du signe  -  si X et Y sont de signes différents.

retour à la liste

Problème, qui se présente (se code) sous la forme d'une écriture en trois temps : premier membre (ou membre de gauche), signe =, et deuxième membre (ou membre de droite) ; les membres de l'équation sont les résultats d'un calcul littéral ou numérique ; une lettre joue un rôle particulier, et on l'appelle l'inconnue, à moins que ce ne soit le cas de plusieurs lettres, qu'on appelle les inconnues ; les autres lettres sont des paramètres (on peut choisir leurs valeurs ; à chaque choix correspond une équation). Le problème peut s'énoncer " résoudre dans tel ensemble l'équation d'inconnue x etc. " ; il s'agit de trouver par quelles valeurs on peut remplacer l'inconnue pour que cette écriture, tous calculs faits, devienne une égalité juste.

Exemple. Résoudre dans R l'équation d'inconnue x : 2 - x = x - 4.

L'école nous apprend assez tôt les règles de transformations licites sur ces écritures, ce qui permet de modifier l'écriture du problème sans en changer les solutions : 6 = 2x , et donc x = 3. Il est désormais évident que la seule valeur que l'on puisse substituer à x pour transformer cette écriture en une égalité vraie est 3, qui est donc la seule solution de l'équation.

Exemple. Résoudre dans N l'équation d'inconnue x : 2 - x = x - 4.

Dans, les propriétés des opérations étant moins bonnes que dans (ou ou ou ...), la résolution de cette équation est moins simple. Par exemple, la soustraction n'est pas toujours possible dans : une solution de l'équation devrait transformer l'écriture en égalité vraie, c'est-à-dire que l'on peut calculer les deux membres, et contrôler qu'ils sont bien égaux ; or le premier membre ne peut se calculer que pour des valeurs de  x situées avant 2 ; et le deuxième membre ne peut se calculer que pour des valeurs de x situées après 4, condition incompatible avec la précédente. Aucune valeur de  x ne pourra faire que les deux membres soient égaux, puisqu'on ne peut pas les calculer simultanément. L'équation n'a pas de solution.

En résumé, le nombre entier 3 est solution de l'équation x : 2 - x = x - 4  formulée dans Z (ensemble des entiers relatifs) mais pas de l'équation formulée dans N car les calculs ne s'y font pas de la même façon.

• On attribue aux équations des qualificatifs plus précis suivant l'ensemble dans lequel on les résout et suivant la nature ou la forme de l'écriture utilisée : équations diophantiennes, polynomiales, algébriques etc.

  algébrique (nombre), diophantien, Fermat, Newton (méthode de),
  premiers entre eux (nombres), racine (d'un polynôme), etc.

retour à la liste

voir barycentre (en Physique)

retour à la liste

Relation binaire (c'est à dire concernant deux objets à la fois) qui permet de classer des objets en regroupant ensemble ceux qui sont en relation. Une relation d'équivalence exprime une idée de ressemblance, de caractéristiques communes, d'appartenance à un même groupe.

Une relation binaire R dans un ensemble E est appelée une relation d'équivalence dans E (on dir aussi sur E) si elle vérifie les trois propriétés suivantes, appelés axiomes des relations d'équivalence :

(1) Réflexivité. Pour tout élément x de E , on a xRx.
(2) Symétrie. Pour tout couple (a,b) d'éléments de E, on a l'implication   aRb bRa
(3) Transitivité. Pour tout triplet (a,b,c) d'éléments de E, on a l'implication (aRb et bRc) aRc

Lorsque que R est une relation d'équivalence sur E, la propriété aRb se lit « a et b sont équivalents (par la relation R) » ou « a est R-équivalent à b » ou encore « a est équivalent à b ».

A toute relation d'équivalence on peut associer des classes d'équivalence : l'ensemble des éléments de E qui sont équivalents à un élément donné x de E s'appelle la classe d'équivalence de x pour la relation R, et est souvent notée.

• Il est facile de voir que deux classes d'équivalences d'une relation d'équivalence R sont soit disjointes soit confondues. Les différentes classes d'équivalences forment ainsi une partition de l'ensemble de départ E. Il est souvent commode de voir les membres de cette partition comme les éléments d'un nouvel ensemble, noté E/R et appelé ensemble quotient de E par la relation R.

Exemple 1. Jeu de cartes. Au jeu des 7 familles, Considéront deux cartes comme "équivalentes" si elles ont la même couleur (jeux de 32 ou 52 cartes usuels) ou si elle représentent des personnages de la même famille (jeux des 7 familles). L'ensemble des cartes d'une même couleur (ou d'une même famille) forme une "classe d'équivalence".

Exemple 2. Classifications animales ou végétales. En Zoologie et en Botanique on classe les animaux et les plantes suivant des caractères communs. Chaque manière particulière de classer correspond à une relation d'équivalence particulière et donne un nom particulier aux "classes d'équivalence" correspondantes : on parle par exemple d'"espèce", mais aussi de "sous-espèce", de "race", de "famille", de "groupe", de "genre", de "classe", d' "ordre", de "genre", etc.

Exemple 3. Courbes de niveau. Convenons que deux points d'une carte géographique sont "équivalents" s'ils représentent des lieux de même altitude. A chaque altitude donné correspond ainsi une "classe d'équivalence". pour les cartes maritimes ou terrestres détaillées, les principales "classes d'équivalences" sont marquées : elles forment des lignes appelées courbes de niveau.

Exemple 4. Congruence entre nombres entiers. Donnons-nous un nombre entier positif n. Dans l'ensemble des entiers relatifs, la relation (x-y est divisible par n) entre deux entiers x et y est une relation d'équivalence. Cette relation, appelée congruence modulo n, est notée sous la forme x y (modulo n), expression que l'on lit « x congru à y modulo n » ou « x et y sont congrus modulo n ». Pour que deux entiers x et y soient congrus modulo n, il faut et il suffit qu'ils aient même reste lorsqu'on les divise par n (voir division euclidienne). Il en résulte que la relation de congruence modulo n partage l'ensemble des entiers relatifs en exactement n classes d'équivalence, les classes de congruence modulo n. L'ensemble quotient correspondant est noté /n ou encore.

Exemple 5. Parallélisme. La relation « (D) est parallèle à (D') » entre droites du plan (ou de l'espace...) est une relation d'équivalence. Les classes d'équivalence sont appelées les directions (de droites). Une direction est ainsi un élément de l'ensemble quotient de l'ensemble des droites du plan (ou de l'espace) par la relation de parallélisme.
En géométrie projective*, on s'intéresse précisément à ces directions. De nouveaux espaces géométriques y sont construits, où les directions de droites sont vus comme ... de simple points ! Les termes usuels de la géométrie habituelle (point, points alignés, droite, angles, distances etc.) y sont redéfinis de manière nouvelle. Si l'on traite par exemple de cette manière l'ensemble des directions des droites de l'espace on obtient un espace géométrique qui ressemble au plan usuel tout en étant assez différent (cet espace géométrique, appelé plan projectif réel*, est un exemple de géométrie non-euclidienne.

Exemple 6. Vecteurs. La relation « les points A,B,D,C du plan (ou de l'espace), pris dans cet ordre, forment les sommets d'un parallélogramme » peut être vue non comme une relation entre quatre points mais comme une relation entre deux couples de points, les couples (A,B) et (C,D). Une telle relation entre couples de points, constitue alors une relation d'équivalence ; les vecteurs du plan (ou de l'espace) peuvent être définis comme les classes d'équivalences associées à cette relation (voir l'article "vecteur" pour d'autres définitions possibles).

retour à la liste

Quand, en mathématiques, on parle de l'espace, sans préciser plus, on parle de la représentation la plus courante de l'espace physique, c'est à dire de l'espace à 3 dimensions où l'on fait de la géométrie euclidienne*: cette géométrie euclidienne est couramment appelée "géométrie dans l'espace".

Bien plus généralement, dès que des éléments et des parties d'un ensemble E peuvent être pensés et étudiés à la manière des points et des figures de cette géométrie dans l'espace, c'est à dire dès qu'interviennent des idées de position ou de situation, de proximité ou d'éloignement, de figure ou de forme, de déplacement ou de mouvement, on parlera de E comme d'un espace et on appellera points ses éléments.

Dans un espace géométrique, on fera de la Géométrie : les problèmes essentiels seront les positions relatives des points, les propriétés des figures que l'on peut construire avec les points, et les moyens de comparer et de transformer ces figures.

Dans un espace métrique, on va pouvoir mesurer des figures et des formes à l'aide d'une distance: à deux points quelconques A,B de l'espace est associé un nombre unique, appelé distance de A à B , un nombre petit ou grand suivant que les points A et B seront proches ou éloignés.

Avec un espace topologique on fera de la Topologie : on va pouvoir bouger les points de manière progressive, déformer les figures de manière élastique, sans séparer les constituants.

retour à la liste

Terme primitif de la Logique mathématique : à partir de deux propositions, A et B, on peut former une nouvelle proposition qui s'écrit (A et B). Par définition, cette proposition (A et B) est vraie si (et seulement si) chacune des propositions A et B est vraie.

Autrement dit, la proposition (A et B) est fausse :
- si A est fausse (peu importe alors la vérité de B)
- si B est fausse (peu importe alors la vérité de A)

La négation de la proposition (A et B), c'est à dire la proposition  non(A et B) , est équivalente à la proposition   (nonA) ou (nonB).

ou

retour à la liste

Qui se rapoort à Euclide ou à la géométrie euclidienne

retour à la liste

Qui se rapoort à Euclide ou à la géométrie euclidienne

retour à la liste

Qui se rapporte à Euclide ou à la géométrie euclidienne

retour à la liste

Une géométrie est dite euclidienne si elle satisfait le 5ème postulat d'Euclide : « Par un point pris hors d'une droite (D), il passe une droite parallèle à (D) et une seule.»

retour à la liste

Portion plane de la surface du polyèdre, délimitée par des arêtes du polyèdre. Deux faces qui se rencontrent se coupent suivant une arête ou un sommet.

polyèdre

retour à la liste

Lorsqu'un élément P s'écrit comme le produit (le résultat d'une multiplication) d'autres objets a, b, c, ... , d (autrement dit si  P = a x b x c x ... x d), chacun des éléments a, b, c, ... , d est appelé un facteur de ce produit.

Le mot " facteur " est surtout utilisé dans les situations où la division n'est pas toujours possible.

Par exemple dans l'ensemble des entiers naturels, 4 est un facteur de 1996. Dans l'ensemble des mots (où la multiplication est la concaténation), le mot " terne " est un facteur de " éternellement " mais pas de " éternuement ".

facteurs premiers, factorisation

retour à la liste

Le produit 1x2x3x...xn des  n premiers nombres entiers positifs est noté  n! et est appelé factorielle n . On convient que factorielle 0 vaut 1, ce qui est en accord avec le théorème suivant :

• Théorème. Pour tout entier naturel n, le nombre de permutations d'un ensemble à n éléments est  n!.
• Tableau des premières valeurs de factorielle n.
  

  n	0	1	2	3	4	5	6	7	8	9	10
  n!	1	1	2	6	24	120	620	4 340	34 720	312 480	3 124 800

• Formule de Stirling. Elle permet le calcul approché de  n! pour n grand :
  , où est une fonction de n qui tend vers 0 lorsque n tend vers +

retour à la liste

Si on peut réécrire une expression algébrique sous forme de produit de facteurs, on dit qu'on factorise cette expression.

produit, facteur

retour à la liste

Le mot famille traduit l'idée de catalogue d'objets, sans ordre particulier, où un même objet peut apparaître plusieurs fois ; les objets ainsi réunis , appelés les membres de la famille (on dit aussi, de manière impropre, les éléments de la famille) sont repérés chacun par une étiquette, souvent appelée indice.

Alors que les éléments d'un ensemble sont tous différents, les membres d'une famille peuvent être répétés plusieurs fois.

Exemple 1. Dans un répertoire d'adresses, à chaque nom correspond une adresse et une seule mais une même adresse peut correspondre à plusieurs noms : au sens mathématique, le répertoire forme une famille dont les membres sont les adresses, chaque nom jouant le rôle d'étiquette.
Par contre pour parler d'une "famille" au "jeu des 7 familles", on emploiera plutôt en mathématiques le mot ensemble que le mot famille, car toutes les cartes d'une même "famille" sont différentes : à des "étiquettes" différentes (le père, la grand-mère, la fille...) correspondent des cartes différentes.

Exemple 2. L'ensemble des carrés des nombres entiers de l'intervalle [-2,+3] est l'ensemble {0,1,2,9}, alors que la famille des carrés des nombres de l'ensemble E={-2, -1 , 0 , +1 , +2 , +3 } est la liste (4 , 1 , 0 , 1 , 4 , 9) , où chacun des nombres 1 et 4 apparaît deux fois.
Cette liste peut se noter ( x² )_xE , ce qui se lit « famille des éléments de la forme x²  pour xappartenant à E ».

On emploi assez souvent le mot famille pour désigner un ensemble dont les éléments sont eux-mêmes des ensembles avec une propriété commune : la famille des tangentes à une courbe, la famille des triangles isocèles rectangles, etc.

Plus précisément, le mot "famille" s'utilise lorsque les objets auquels on s'intéresse sont repérés par les éléments d'un autre ensemble donné I: à chaque élément  i de  I correspond un membre bien défini  f_i de la famille. Autrement dit, les membres d'une famille sont les images des éléments d'un ensemble donné  I par une application  f  définie sur  I. Une telle famille se note sous la forme ( f ( i) )_iI ou encore ( f_i)_iI  ; les éléments (distincts) de I ainsi placés en indice jouent le rôle d'étiquette:

Pour parler des objets qui vérifient une propriété donnée, on utilise plutot les mots ensemble, collection, ou classe.

retour à la liste

Pierre Fermat, 1601-1665, Conseiller du Roi au Parlement de Toulouse, " prince des amateurs en mathématiques ", avait l'habitude d'écrire des notes dans les marges de ses livres (oh !) et d'y énoncer des théorèmes sans démonstration, dont beaucoup se révélèrent justes et beaucoup d'autres se révélèrent faux.

Il a ainsi inscrit (en latin) en marge d'un problème de Diophante (résolution en nombres rationnels de l'équation x² + y ² = z² ) :

" Tout au contraire, il est impossible de partager un cube en deux cubes, une quatrième puissance en deux quatrièmes puissances ou, en général, une puissance quelconque de degré supérieur à deux en deux puissances du même degré ; j'ai découvert une démonstration vraiment admirable (de ce théorème général) que cette marge est trop petite pour contenir. "

C'est-à-dire que l'équation diophantienne Xⁿ + Y ⁿ = Z ⁿ n'a pas de solution (en nombres entiers) si n > 2.

Cet énoncé est le seul de Fermat qui ait résisté à tous les mathématiciens pendant 350 ans. Connue comme le " grand théorème de Fermat " ou " le dernier théorème de Fermat ", cette conjecture est devenue le " Théorème de Wiles-Taylor " depuis qu'Andrew Wiles en a donné une démonstration en juin 1993 (démonstration qui contenait un " trou ", comblé avec l'aide de Taylor en octobre 1994).

retour à la liste

Un ensemble de points est fermé si tous les points qui ne lui appartiennent pas lui sont extérieurs, autrement dit si son ensemble complémentaire est ouvert.

retour à la liste

Une figure géométrique est composée de plusieurs objets géométriques satisfaisant à certaines règles qui énoncent des relations entre ces objets.

Les objets géométriques (points, droites ou portions de droites, courbes ou portions de courbe, plans, portions de plan ou d'espace etc.) qui composent une figure sont appelés les éléments constitutifs de la figure. Toute figure géométrique est le résultat d'une construction : certains éléments de la figure sont donnés en début de la construction, les autres éléments sont définis pas à pas : à chaque étape de la construction, le nouvel élément introduit est déterminé sans ambiguité par des relations qui mettent en jeu les éléments donnés ou construits précédemment.

• Dans le langage courant, le mot "figure" désigne le dessin qui représente une figure géométrique. Ces dessins, qui aident à comprendre les propriétés des figures, peuvent être trompeurs, c'est pourquoi l'on dit souvent : « il ne faut pas raisonner sur la figure ».

retour à la liste

Un ensemble est fini si on peut compter ses éléments, 1, 2, 3, ..., sans dépasser un nombre entier naturel donné. Le dernier nombre utilisé dans le comptage est le nombre d'éléments (on dit aussi la cardinalité) de l'ensemble.

En Théorie des Ensembles* on introduit en même temps les notions d'ensemble fini et de nombre entier naturel : un ensemble E est fini s'il n'existe aucune bijection de E sur un sous-ensemble strict de E. Les cardinaux des ensembles finis sont appelés les nombres entiers naturels.

dénombrable , infini , nombre entier naturel

retour à la liste

Le terme mathématique expime l'idée courante de dépendance. On parle de fonction lorsqu'on associe de manière systématique quelque chose (un "résultat") à d'autres choses (des "données"), le but étant d'étudier comment le résultat dépend des données, c'est à dire comment le résultat change lorsque que les données changent.

Exemples : évolution du nombre de chômeurs en fonction du temps, couleur d'une galaxie en fonction de sa vitesse de fuite, température d'ébullition de l'eau en fonction de la pression, évolution de la taille en fonction de l'individu et du temps.

Une fonction est un procédé de définition, de construction, qui permet, pratiquement ou théoriquement, de fabriquer quelque chose de nouveau avec des éléments connus, pourvu que les "conditions de fabrication" soient réunies.

Chaque fois qu'on veut indiquer qu'un objet O est formé à partir d'autres, et que l'on souhaite indiquer que les objets x, y, z, ... interviennent dans cette construction, on dit que O est fonction de x, y, z, ... . Si la construction est désignée par la lettre C, on écrit O = C(x, y, z, ...).

retour à la liste

Le mot « géodésique » exprime l'idée de plus court chemin, mais de manière plus générale. Sur une surface courbe, un élastique tendu entre deux points prend la forme d'une géodésique de la surface. Lorsqu'on se déplace sur une surface en allant toujours "droit devant soi", on décrit une géodésique (on dit aussi une ligne géodésique).

Dans un espace où l'éloignement de deux points quelconques peut être mesuré (espace métrique), on appelle géodésique une ligne qui a localement les caractéristiques d'un plus court chemin : précisément, un arc géodésique (on dit aussi une courbe géodésique, ou simplement une géodésique) est une courbe C, fermée ou non, qui a la propriété suivante: chaque point P de C peut être placé entre deux autres points A et B de C, de façon à ce que la partie de C située entre A et B soit un plus court chemin de A à B.

L'arc de courbe (AB)C , c'est à dire la partie de la géodésique C qui est comprise entre A et B, contient le point P et constitue un plus court chemin entre A et B.

• Le mot "géodésique" tout seul s'emploie surtout pour une courbe géodésique qu'on ne peut pas prolonger, c'est à dire qui n'est pas un arc d'une courbe géodésique plus longue.
• Un plus court chemin entre deux points donnés est toujours un arc géodésique. Mais la réciproque est inexacte.

Exemple Sur la surface de cette boîte, la ligne brisée AabB est un arc géodésique sans être un plus court chemin entre A et B. La courbe fermée constitué par le bord du rectangle AabB est une géodésique de la surface.

Dans le plan ou l'espace de la géométrie euclidienne, les géodésiques sont les droites et le plus court chemin entre deux points est unique : c'est le segment de droite qui les joint. Il n'en va pas de même pour d'autres géométries où le plus court trajet n'est en général ni droit, ni unique.

Exemples

- Dans le métro, où les trajets sont mesurés par un nombre de stations, il a fréquemment plusieurs plus courts trajets.
- Sur la Terre il y a une infinité de plus courts chemins entre le pôle nord et le pôle sud : ce sont les méridiens.
- Lorsqu'on enroule un fil tendu sur une tige cylindrique, on place le fil sur une géodésique de la surface de la tige. La longueur de fil utilisé entre deux points dépend du nombre de tours effectués pour les joindre.
- Plongeons une règle dans l'eau : elle nous apparaît brisée en deux morceaux qui se rejoignent à la surface de l'eau, le morceau immergé nous semblant plus court qu'auparavant. En effet, la lumière adoptant des vitesses différentes dans l'eau et dans l'air, le plus court chemin (mesuré par le temps de parcours) n'est plus la ligne droite : les rayons luminueux changent de direction à la surface de l'eau, ce qui modifie l'aspect habituel de notre règle.
- Dans notre Univers, les corps célestes massifs courbent la trajectoire de la lumière. Cela explique pourquoi certaines étoiles nous apparaîssent sous forme d'une image double : leur lumière, déviée par un objet massif, nous parvient par deux tralets différents, en suivant deux géodésiques distinctes de l'espace, toutes deux courbes.

retour à la liste

Science de la mesure de la Terre dans l'Antiquité (le mot géométrie est d'origine grecque : "Géo"-"métrie" = "Terre"-"mesure".] la Géométrie (avec un "G" majuscule) désigne maintenant un vaste ensemble de domaines mathématiques qui mettent en jeu les idées de position, d'éloignement, d'espace et de mouvement. Typiquement, la démarche géométrique manipule des objets élémentaires, appelés points et les organise en objets plus complexes appelés figures ; elle évalue les positions et les figures au moyen de mesures et met en relation les figures au moyen de transformations portant sur les points.

En fait, pour cette étude des figures et des transformations, plusieurs théories mathématiques spécialisées se sont développées autour de formes particulières (géométries sphérique, torique, ...) ou mettant en valeur des techniques (géométrie analytique, géométrie différentielle, ...), des conventions ou des règles particulières (géométries finies, géométries projectives, géométries non euclidiennes, ...) : chacune de ces théories est qualifiée par le mot "géométrie" (sans majuscule). L'ensemble des points considérés par une géométrie donnée prend le nom d'espace.

On parlera par exemple de géométrie sphérique* pour nommer l'étude des figures formées par des points à la surface d'une sphère, de géométrie affine* pour nommer l'étude des alignements de points indépendamment des questions de mesure de longueurs ou d'angle, de géométrie différentielle* pour nommer l'étude métrique des formes courbes, etc.

"La Géométrie" étudiée en classe de mathématiques est une géométrie particulière, la géométrie de l'espace euclidien ou géométrie euclidienne* : les figures de bases y sont les droites, soumises au "postulat des parallèles", les transformations essentielles y sont les isométries, qui préservent les distances entre points, et plus généralement les transformations affines, qui préservent l'alignement des points.

Si la géométrie euclidienne s'avère la plus commode pour décrire l'espace terrestre, on fait appel à d'autres géométries pour décrire l'Univers astrophysique (géométries de Minkowski*, géométries riemanniennes*, etc.), conformément aux principes de la relativité énoncés par Einstein.

retour à la liste

Le mot "graphe" renvoie toujours à l'idée de relation entre deux choses, c'est à dire de relation binaire*).

Graphe d'une fonction. Lorsqu'une relation entre deux variables x et y est définie par une fonction f, sous la forme y = f(x), on appelle graphe de f l'ensemble des points M(x ; y) de coordonnées x et y qui vérifient cette relation, c'est-à-dire tels que y = f(x).

Graphe d'une relation. Lorsqu'on s'intéresse à une relation binaire R(x, y) entre deux variables prises dans un même ensemble  E, on appelle graphe de R l'ensemble des couples (x, y) qui vérifient R, c'est-à-dire tels que R(x, y) soit vraie : le graphe de R est ainsi une partie du produit cartésien Ex E.

Une théorie mathématique étudiant les graphes* s'est développée sous le nom de théorie des graphes.

retour à la liste

La théorie des graphes étudie l'organisation d'éléments liés par des contraintes binaires (contraintes qui portent sur deux éléments). on représentent souvent les éléments par des points et les contraintes par des lignes joignant ces points : chaque ligne particulière relie deux points particuliers. La donnée d'un graphe équivaut à celle d'une relation binaire*.

Par exemple, on modélise par un graphe u, un plan de ville où des rues relient des carrefours, une généalogie où des personnes sont liés par parenté, un emploi du temps où des salles sont à apparier avec des classes, une molécule chimique où des liaisons associent les atomes par paires, un carnet d'adresse où des noms sont reliés à des numeros de téléphones, une carte politique où des pays peuvent être "voisins" (deux pays sont voisins s'il ont une frontière commune) etc.

Un graphe est formé de deux types d'objets : des éléments appelés sommets, que l'on représente souvent par des points, et des paires de sommets, appelées arêtes. Dans un multigraphe, une même paire de sommets peut apparaître plusieurs fois.

Dans un graphe non orienté, l'ordre des deux sommets qui composent une arête n'a pas d'importance (exemple d'un réseau de rues à double sens).

Une arête acomposée de deux sommets x et y  se note sous la forme{ x,y} ou [ x, y] ou [ xy] : on a { x,y}={ y,x}. On dit l'arête a relieou jointles sommets xet y ou encore que a est une arête entre xet y ou a pour extrémités xet y, Il est permis que x et y soient confondus, auquel cas , a est appelée une boucle. Si deux sommets x et y sont reliés par une arête, on dit qu'ils sont voisins ou adjacents.

Dans un graphe orienté, l'ordre des deux sommets qui composent une arête est important (exemple d'un réseau de rues à sens unique) : chaque arête a un sens précis de parcours et s'appelle une arête orientée ou arc.

Formellement, un graphe est noté sous la forme  G= ( S, A) :  S est l'ensemble des sommets, A est la famille des arêtes (orientées ou non). Pour un graphe non orienté, les éléments de A sont des paires de sommets, pour un graphe orienté, ce sont des couples de sommets. 

Graphe simple, multigraphe. On dit qu'un graphe est simple lorsque deux éléments voisins quelconques sont liés par une seule arête (ou un seul arc dans le cas orienté) ; autrement dit, toutes les arêtes (les arcs dans le cas orienté) sont distinctes et A est un ensemble de paires (de couples dans le cas orienté). Au contraire, dans un multigraphe, deux sommets quelconques peuvent être liés par plusieurs arêtes (ou plusieurs arcs) : A est une famille de paires (ou de couples).

graphe, arête, sommet, relation binaire

retour à la liste

Notion mathématique issue de l'expérience physique et qui traduit l'idée de position moyenne.

o En géométrie euclidienne, on définit le centre de gravité (mathématique) d'un ensemble fini de points comme l'isobarycentre de ces points, c'est à dire le barycentre de ces points affectés de coefficients égaux.

On démontre que le centre de gravité de deux points A et B est le milieu du segment [AB] et que le centre de gravité G de trois points A,B,C est le point de concours des trois médianes du triangle ABC (ce point G est aussi appelé centre de gravité du triangle ABC).

On peut (en utilisant le calcul intégral*) généraliser cette définition à des ensembles composés d'une infinité de points : des lignes, des surfaces, des volumes etc.

Pour déterminer mathématiquement le centre de gravité de lignes, de surfaces ou de volumes, on se sert souvent de l'idée simple suivante (fondamentale en Analyse): on détermine un résultat approché et on passe à la limite :

1) on découpe la forme en un nombre fini de petits morceaux que l'on assimile chacun à un point affecté d'un coefficient (qui indique son aire ou son volume)

2) on prend le barycentre B des ces points avec ces coefficients. Plus les morceaux sont petits et plus le nombre de morceaux est élevé plus le point B s'approche d'un point bien déterminé, appelé le centre de gravité de la forme.

La technique qui permet de faire correctement ce passage à la limite s'appelle le calcul intégral*.

Exemple du triangle : on démontre que le centre de gravité G d'un triangle ABC coïncide avec le centre de gravité de la surface triangulaire ABC. Par contre, sauf cas très particulier, le centre de gravité du bord du triangle (réunion des trois segments [AB], [BC] et [CA]) ne coïncide pas avec avec le point G.

retour à la liste

syn. contenu. Un ensemble A est inclus dans un ensemble B, et on note AB, si tout élément de A appartient à B.

est le symbole d'inclusion.

On dit que A est strictement inclus dans B si A est inclus dans B mais est différent de B.

Tout ensemble inclus dans un ensemble E est appelé une partie de E.

retour à la liste

retour à la liste

Le mot vient du préfixe in (négation) et du mot latin finis (limite, bord) : est infini ce qui est sans fin , sans limite. Un ensemble infini est un ensemble qui n'est pas fini. Intuitivement, un ensemble est infini si son "nombre d'éléments" (voir cardinal) ne change pas lorsqu'on lui enlève un élément ou lorsqu'on lui ajoute un nouvel élément. Un ensemble infini a "plus" d'éléments que n'importe quel ensemble fini.

• En théorie des ensembles*, les notions d'ensemble fini et d'ensemble infini deviennent rigoureuses grâce à la notion de bijection : un ensemble E est infini s'il existe une bijection de E sur un sous-ensemble strict de E. L'existence d'ensembles infinis est assurée par un axiome, l'axiome de l'infini, qui permet par exemple de parler de l'ensemble des nombres entiers naturels.

Exemple : L'application qui à chaque entier naturel n fait correspondre son successeur n +1 est une bijection de l'ensemble des nombre entiers naturels = {0,1,2,...} sur le sous-ensemble strict des nombres entiers naturels positifs ^*={1,2,...}. L'ensemble est donc infini.

Citation : " Deux choses sont infinies : l'univers et la bêtise humaine ; mais en ce qui concerne l'univers, je n'en ai pas encore acquis la certitude absolue. "  [Albert Einstein]

cardinal, dénombrable , fini, nombre entier naturel

retour à la liste

Intuitivement, un point est intérieur à une figure s'il est "entouré" par des points de la figure. On emploi surtout le mot "intérieur" à propos de courbes fermées dans le plan (par exemple un cercle, ou une ellipse ; mais un polygone peutêtre vu aussi comme une courbe fermée), ou de surfaces fermées dans l'espace (une sphère, un cube etc.).

Exemple. Les courbes fermées planes usuelles partagent le plan en deux régions dont l'une est bornée. Cette région bornée est alors appelée l'intérieur de la figure.

On emploi aussi le mot "intérieur" pour des ensembles convexes ou plus généralemnt pour des figures ou formes géométriques qui sont vues comme des ensembles de points: la définition précise d'intérieur dépend de l'espace ambiant et aussi de la manière dont est définie la figure.

• Exemple1. Si l'espace ambiant est une droite, l'intérieur d'un segment [AB], dans cette droite, est le segment ouvert ]AB[ formé des points du segment [AB] autres que A et B. Par contre si l'espace ambiant est le plan, aucun point n'est intérieur à un segment [AB] : l'intérieur d'un segment est vide.
• Exemple2. Dans le plan, l'intérieur d'un cercle (C) de centre O et de rayon r est le disque ouvert formé des points dont la distance à O est inférieure (strictement) à r : le cercle est vu ici comme une courbe fermée. Par contre si on considére (C) comme un simple ensemble de points : sont intérieur sera alors l'ensemble vide.
  

• Pour définir l'intérieur de figures convexes dans un espace géométrique*, on s'appuie sur la notion de segment.
• Pour des figures dans un espace métrique*, on s'appuie sur la notion de distance.
• Pour des figures dans un espace topologique*, on s'appuie sur la notion d'ensemble ouvert.

Intérieur (d'un triangle)

Un triangle du plan partage le plan en trois parties disjointes: le bord du triangle, son intérieur, son extérieur.

• Un point du bord est un point qui appartient à au moins un des cotés du triangle.
• Un point intérieur (au sens strict) est un point M qui 1°) n'est pas sur le bord, 2°) est sur un segment qui joint deux points du bord. On dit des points intérieurs qu'ils sont dans le triangle.
• Un point est extérieur s'il n'est ni intérieur ni sur le bord. On dit des points extérieurs qu'ils sont hors du triangle.

On démontre que l'intérieur strict d'un triangle est l'intersection des trois demi-plans ouverts qui contiennent ce triangle et qui s'appuient sur ses cotés.

Intérieur , extérieur (d'un cercle)

Dans le plan, l'intérieur d'un cercle (C) de centre O et de rayon r est le disque ouvert formé des points dont la distance à O est inférieure (strictement) à r . Les points dont la distance à O est supérieure à r forment l'extérieur de(C). Le cercle est vu ici comme un exemple de courbe fermée.

Intérieur , extérieur (d'une courbe fermée)

Une courbe simple fermée plane usuelle (un cercle, une ellipse, le bord d'un polygone etc. , plus généralement toute courbe de Jordan*) partage les points du plan en trois catégories : il y a les points qui sont sur la courbe, les points qui sont intérieurs à la courbe, ceux qui lui sont extérieurs.

• Pour définir précisément ces notions sans recourrir à la figure, on peut par exemple procéder de la manière suivante :
  • On place la courbe (K) à l'intérieur d'un grand cercle (C) (cela est possible car la courbe est fermée).
  • Tout point situé à l'extérieur du cercle (C) sera dit extérieur à (K) .
  • Tout point qui peut être relié à un point extérieur à (K) par une ligne (une autre courbe) qui ne rencontre pas (K) sera dit extérieur à (K)
  • Tout point qui n'est pas sur la courbe (K) ni extérieur à (K) en vertu des règles précédentes est dit intérieur à (K).

  En résumé, lorsque (K) est une "bonne" courbe fermée, elle partage le plan en deux régions dont une est bornée : c'est cette région bornée qui est appelée l'intérieur de la figure.

• Il existe des "mauvaises" courbes fermées, où la notion d'intérieur n'a plus vraiment de sens : Peano et Hilbert, par exemple, ont construit des courbes qui remplissent tout un carré !

Intérieur (d'un ensemble convexe)

Voir bord d'un ensemble convexe.

Intérieur (d'un ensemble de points)

Un point p est intérieur à un ensemble A si p et tous les points situés "très proches" de p appartiennent aussi à l'ensemble A. L'ensemble des points intérieurs à A s'appelle l'intérieur de A et se note souvent. C'est un ensemble ouvert*.

• On peut donner un sens précis à cette définition si on dispose d'une distance. Un point p est intérieur à A s'il existe un nombre réel positif r tel que tous les points dont la distance à p est inférieure à  r appartiennent à A, soit formellement si :
  (r> 0 ) (x) [(distance(x,p)<e) (xA)]

• L'intérieur d'un ensemble convexe peut être défini sans parler de distance (voir bord d'un ensemble convexe)
  
• Plus généralement, dans un espace topologique* E, un point p est intérieur à A s'il appartient à un ouvert de E contenu dans A. L'intérieur de A est alors la réunion des ensembles ouverts contenus dans A.

retour à la liste

Opération portant sur des ensembles qui à deux ensembles A et B associe l'ensemble AB (lire «A inter B»), formé des éléments communs à A et à B, c'est à dire qui appartiennent à A et à B. L'ensemble AB est appelé l'intersection des ensembles A et B.

Exemples : {1,2,3}{2,3,4,5} = {2,3} . Dans , on a [-1 ; 2]  ]-5 ; 1[ = [-1 ; 1[ .
L'intersection de deux droites (D) et (D') du plan peut être

- vide (si (D) et (D') sont parallèles et différentes)
- une droite (si (D) et (D') sont confondues)
- ou un ensemble réduit à un unique point (dans les autres cas).

Pour tout ensemble A, on a AA = A

L'intersection ensembliste est une opération associative et commutative.

(Identité de de Morgan) L'intersection ensembliste est distributive par rapport à l'union ensembliste, autrement dit on a l'identité suivante : A(BC)=(AB)(AC)

L'intersection de plusieurs ensembles A, B, C, ...  est l'ensemble formé des éléments qui appartiennent à tous les ensembles A, B, C, ...

• Si ( E_i)_iI est une famille d'ensembles, le nouvel ensemble formé des éléments qui appartiennent à tous les ensembles  E_i est appelé l'intersection (des ensembles) de la famille. et se note. Cet ensemble est donc défini par :
  

  théorie des ensembles*, union, réunion

retour à la liste

Si le produit de deux nombres vaut 1, on dit que ces nombres sont inverses l'un de l'autre.

Plus généralement, dans tout ensemble E où l'on dispose d'une multiplication, notée x, qui admet une unité notée 1 ( élément neutre à droite et à gauche), on dit que deux éléments a et b sont inverses l'un de l'autre si on a axb = bxa = 1. On dit aussi que b est un inverse de a. (a est aussi un inverse de b). Un élément qui admet un inverse est dit inversible.

Dès que la multiplication est associative, chaque élément a admet au plus un élément inverse. S'il existe, cet élément inverse est simplement appelé l'inverse de a et est noté ou ou encore 1/a,

Dans un groupe multiplicatif, tout élément a de E est inversible.

Remarque. Lorsque plusieurs opérations interviennent sur un même ensemble E, il faudra bien préciser lorsqu'on parlera d'élément symétrique de quelle opération il s'agit. En particulier on évite de parler d'utiliser le mot "inverse" lorsque l'opération considérée est une addition, avec pour élément neutre 0 [voir addition] : lorsque a+b = b+a = 0 on dira que a et b sont des éléments opposés.

Exemple : dans l'ensemble des nombres réels. tout élément x a un opposé -x (élément "symétrique" pour l'addition) et 0 est son propre opposé. Mais 0 n'a pas d'inverse (pour la multiplication). Le nombre 0,333333... est l'inverse de 3 (pour la multiplication) et peut être noté sous la forme , 1/3 ou 3^-1.

retour à la liste

Un élément, est dit inversible s'il admet un inverse.

retour à la liste

Nombre réel qui n'est pas rationnel. Voir rationnel (nombre)

retour à la liste

retour à la liste

Syn. centre de gravité . L'expression "centre de gravité" est employée en physique, alors que le mot isobarycentre est plutôt utilisé en mathématiques.

retour à la liste

Théorème utilisé dans la démonstration d'autres théorèmes.

retour à la liste

Une fonction f associe une valeur f(x) à une valeur variable x. Comment se comporte f(x) lorsque le nombre variable x s'approche d'une valeur particulière a ? Il se peut qu'au fur et à mesure que x s'approche de a, f(x) se rapproche d'une valeur particulière b ; dans ce cas cette valeur b est unique, et on dit que b est la limite de la fonction f en a. ou que f(x) tend vers b lorsque xtend vers a et on écrit :

   ou       ou encore    

Remarque. Que la fonction soit définie ou non pour la valeur a de la variable x, peu importe ; ce qui est intéressant c'est de pouvoir dire quelque chose sur f(x) lorsque la variable x "n'est pas loin" de a. Dire que b est limite de f en a revient à dire que b est une valeur "acceptable" pour f(x) dès que x est suffisamment proche de a. Si f est défini en a, alors nécessairement f(a)=b. Si f n'est pas définie en a, on peut étendre la définition de f en a posant f(a)=b (on dit dans ce cas qu'on prolonge f en a par continuité).

Une valeur limite n'est pas toujours calculable excatement, même si le calcul de f(x) ne pose pas problème. Mais, par définition, une limite est toujours calculable de manière approchée , quelle que soit la précision souhaitée. En effet dire que f(x) a pour limite b lorsque x tend vers a, c'est dire que pour calculer b avec un nombre imposé de décimales exactes, il suffit de connaître un certain nombre de décimales exactes pour a : si a' est une valeur suffisamment approchée de a, f(a') sera une bonne valeur approchée pour b.

L'idée d'approximation et de valeurs approchées permet de rendre rigoureuse la définition d'une limite, lorsque que l'on dispose d'une notion de distance permettant de mesurer l'écart entre deux valeurs et en donner ainsi un sens mathématique au mot "approché". Dire que f(x) a pour limite b lorsque x tend vers a, revient à affirmer l'existence d'une suite de nombres a₀, a₁ , a₂ , qui fournissent des garanties successives pour le calcul des décimales successives du nombre b :

dès que l'écart entre x et a est inférieur à une certaine valeur, a₀, l'écart entre f(x) et b est inférieur à 1 ;
dès que l'écart entre x et a est inférieur à une autre valeur, a₁, l'écart entre f(x) et b est inférieur à 1/10 ;
dès que l'écart entre x et a est inférieur à une autre valeur, a₂, l'écart entre f(x) et b est inférieur à 1/100 ;
... et ainsi de suite, indéfiniment.

En résumé, pour tout nombre entier k, dès que l'écart entre x et a est inférieur à une certaine valeur, a_k, l'écart entre f(x) et b est inférieur à 1/10^k.

Avec une distance, on peut reformuler de manière générale le processus précédent par la définition suivante.

Définition. Soient f une fonction d'un espace métrique E vers une autre espace métrique F, a un élément de E, b un élément de F. On dit que f(x) a pour limite b lorsque x tend vers a si on a la propriété suivante :

(e > 0) ( a > 0) [ ( f(x) est définie  et  distance(x, a) < a)  distance(f(x), b) < e ]

Dans cette définition, e et a sont des réels représentant respectivement l'erreur tolérée sur b et la marge d'erreur qu'on peut s'accorder sur a, la distance de x à a étant mesurée dans E, la distance de f(x) à b dans F.

limites infinies. On peut dire qu'un nombre est "voisin" de +s'il est au delà de "la barre" que l'on se fixe (ce peut être 3 m pour un sauteur, 10 m pour un perchiste) ; de même pour -, s'il est en deçà de la barre que l'on se fixe (ce peut être -10 000 m pour une baleine, -500 m pour un plongeur) ; de même pour un point proche de l'infini (+et -si on travaille sur la droite,pour le plan, l'espace) s'il est suffisamment loin d'un point de référence (hors de la feuille où on dessine, à une distance de plus d'une année-lumière de la terre, etc).

Définition générale (pour une fonction f: EF, où E et F sont des espaces topologiques*, avec Déf(f) pour domaine de définition). Grâce à la notion de voisinage, on a une définition plus simple des limites (qui couvre tous les cas, en particulier lorsque a ou b sont +ou -) :

ssi ( B, voisinage de b dans F) ( A, voisinage de a dans Déf(f)) (xAf(x)B).

retour à la liste

Lorsque le terme général s_n d'une suite tend à se rapprocher d'une valeur particulière L au fur et à mesure que n augmente, on dit que la suite ( s_n ) a pour limite L lorsque  n tend vers + , ou encore que la suite ( s_n) converge vers L.

Plus présicément, une suite ( s_n ) peut être vue comme une fonction s qui associe à chaque entier naturel n le nombre s_n . La suite ( s_n) a pour limite L lorsque  n tend vers +si la fonction s a pour limite L lorsque n tend vers +(voir limite d'une fonction).

On parle de limite pour des suites de nombre réels ou de nombres complexes, et plus généralement pour des suites de points pris dans un espace métrique ou dans un espace topologique.

retour à la liste

Mot mathématique synonyme d' opération quelconque. Une loi de composition peut porter sur des éléments de même nature (loi de composition dite interne) ou de nature différente (loi de composition dite externe).

retour à la liste

retour à la liste

Quadrilatère plan non croisé ayant 4 cotés égaux.

retour à la liste

Un majorant est tout simplement quelque chose qui est plus grand, qui majore ! Evidemment, il faut encore savoir ce que signifie "plus grand".

• Il peut s'agir de nombres. En particulier, quand on cherche un nombre, ou qu'on le calcule avec des formules, on a souvent du mal à obtenir le résultat exact, et il est parfois utile d'avoir au moins un encadrement. On cherche alors un majorant (un nombre plus grand) et un minorant (un nombre plus petit).
  Exemple de "factorielle n" : n! = 1 x 2 x 3 x ... x (n-2) x (n-1) x n a pour majorant n^n-1. Le nombre n^n-1 est évidemment beaucoup plus grand que n!, mais il est plus simple à manipuler dans certains cas, par exemple si on travaille sur des inégalités qui font intervenir n! .
• Il peut aussi s'agir d'ensembles : un ensemble, A, est un majorant pour un autre, B, si le premier (A) contient le second (B), c'est-à-dire si B est inclus dans A.

  Il y a lieu de se méfier : deux ensembles A et B ne sont pas forcément comparables, loin de là (exemple : l'ensemble des nombres compris entre 0 et 2 et l'ensemble des nombres compris entre 1 et 3 ... aucun des deux n'est contenu dans l'autre).

• Un nombre, M, peut aussi être un majorant pour un ensemble de nombres, A : si M est majorant de tout nombre a de l'ensemble A.
  Par exemple, 2 est un majorant de l'ensemble A des nombres rationnels dont le carré est plus petit que 2. N'importe quel nombre plus grand que 2 sera aussi un majorant ; mais il existe aussi des nombres plus petits que 2 qui sont des majorants de A, par exemple 1,5 (un nombre a de A est soit négatif, soit positif et de carré plus petit que 2 donc aussi plus petit que 2,25 qui est le carré de 1,5 : a 0, ou 0 a et a² 1,5² donc 0 a 1,5). 1,4 n'est pas un majorant de A car 1,41 est dans A et 1,41 n'est pas majoré par 1,4.

  On peut chercher si parmi les majorants de A il y en a un qui est plus petit que tous les autres : c'est ce qu'on appelle la "borne supérieure" de A. Il n'est pas évident que cette borne supérieure existe.

  Si on ne s'autorise que les nombres rationnels, l'ensemble des rationnels dont le carré est inférieur à 2 n'a pas de borne superieure. Si on s'autorise les réels, l'ensemble des rationnels dont le carré est inférieur à 2 a une borne supérieure : c'est .

  minorant.

retour à la liste

Médianes d'un triangle ABC : droite passant par un sommet S du triangle et par le milieu I du coté opposé à S. On donne aussi le nom de médiane au segment [SI] ou à sa longueur SI.

Dans le plan, les trois médianes d'un triangle sont concourantes. Le point de concours est le centre de gravité du triangle.

Médiane d'un quadrilatère ABCD : droites joignant les milieux, I et J, de deux cotés opposés. On donne aussi le nom de médiane au segment [IJ] ou à sa longueur IJ.

(Théorème de Varignon) Dans le plan, les milieux d'un quadrilatère sont les sommets d'un parallélogramme. Autrement dit, les deux médianes d'un quadrilatère se coupent en leur milieu. Ce milieu commun est aussi le centre de gravité des 4 points A,B,C et D.

retour à la liste

Un minorant est tout simplement quelque chose qui est plus petit, qui minore ! Evidemment, il faut encore savoir ce que signifie plus petit.

• Il peut s'agir de nombres. En particulier, quand on cherche un nombre, ou qu'on le calcule avec des formules, on a souvent du mal à obtenir le résultat exact, et il est parfois utile d'avoir au moins un encadrement. On cherche alors un majorant (un nombre plus grand) et un minorant (un nombre plus petit).
  Exemple de "factorielle n" :
  n! = 1 x 2 x 3 x ... x (n-2) x (n-1) x n a pour minorant 2^n-1.
  2^n-1 est évidemment beaucoup plus petit que n!, mais il est plus simple à manipuler dans certains cas, par exemple si on travaille sur des inégalités qui font intervenir n!.
• Il peut aussi s'agir d'ensembles : un ensemble, A, est un minorant pour un autre, B, si le premier (A) est contenu dans le second (B), c'est-à-dire si A est inclus dans B.

  Il y a lieu de se méfier : deux ensembles A et B ne sont pas forcément comparables, loin de là (exemple : l'ensemble des nombres compris entre 0 et 2 et l'ensemble des nombres compris entre 1 et 3 ... aucun des deux n'est contenu dans l'autre).

• Un nombre, M, peut aussi être un minorant pour un ensemble de nombres, A : si M est minorant de tout nombre a de l'ensemble A.
  Par exemple, 1 est un minorant de l'ensemble A des nombres rationnels dont le carré est plus grand que 2. N'importe quel nombre plus petit que 1 sera aussi un minorant ; mais il existe aussi des nombres plus grands que 1 qui sont des minorants de A, par exemple 1,4 (un nombre a de A est de carré plus grand que 2 donc aussi plus grand que 1,96 qui est le carré de 1,4). 1,5 n'est pas un minorant de A car 1,42 est dans A et 1,42 n'est pas minoré par 1,5.

  On peut chercher si parmi les minorants de A il y en a un qui est plus grand que tous les autres : c'est ce qu'on appelle la "borne inférieure" de A. Il n'est pas évident que cette borne inférieure existe.

  Si on ne s'autorise que les nombres rationnels, l'ensemble des rationnels dont le carré est supérieur à 2 n'a pas de borne inferieure. Si on s'autorise les réels, l'ensemble des rationnels dont le carré est supérieur à 2 a une borne inférieure : c'est .

  Voir majorant.

retour à la liste

Suite de symboles appelés lettres. Les modèles mathématiques où on utilise les mots sont souvent appelés des langages. Ils comportent des règles qui permettent de former des mots particuliers à partir de lettres prises dans un ensemble de base appelé alphabet. Ces règles de base constituent alors ce qu'on appelle une grammaire (on utilise aussi le mot automate*) ...

Un langage particulier peut être aussi défini autrement, en listant des propriétés caractéristiques communes aux mots de ce langage.

Exemple. Les palindromes sont les mots (ou les phrases, on ignore alors les espaces, signes de ponctuation et typographies particulières des lettres) qui ne changent pas lorsqu'on les lit à l'envers. Exemples : "non", "radar", "serres", "mon nom", "A man, a plan, a canal : Panama", "Esope reste ici et se repose". On peut engendrer le langage des palindromes avec la grammaire formé des deux règles suivantes :

• le mot vide est un palindrome ;
• si p est un palindrome et si a est une lettre quelconque le mot apa est un palindrome.

retour à la liste

Opération entre entiers naturels qui aux nombres a et b fait correspondre leur produit, noté ax b (noté aussi  ab s'il n'y a pas de risque de confusion).
Par extension, on appelle multiplication toute opération qui généralise cette addition entre nombres entiers.

Exemples. On parlera de produit et de multiplication pour des nombres rationnels, réels, complexes etc., des vecteurs, des transformations géométriques, des fonctions, des polynômes, des matrices, etc.

• D'un manière formelle, la multiplication des entiers naturels se définit à l'aide du produit cartésien d'ensembles.

On utilise encore le mot "multiplication" (ainsi que les mots qui sont usuellement définis à partir cette opération comme : produit, facteur, divisible, division, multiple, quotient, inverse etc.) pour toute opération qui est associative et qui est distributive par rapport à une autre opération, elle-même commutative et associative (cette seconde opération est alors appelée addition (par exemple dans les anneaux, les corps* et les algèbres*).

On utilise enfin le mot multiplication pour désigner une opération quelconque portant sur les éléments d'un ensemble (une loi de composition interne*), surtout lorsque cette opération est associative mais n'est pas commutative (par exemple dans les groupes non abeliens*)

retour à la liste

Ensemble des nombres entiers naturels.

retour à la liste

Ensemble des nombres entiers naturels différents de 0.

retour à la liste

Un 8-uplet, ou 8-uple est une suite qui comporte 8 termes. Un n-uplet ou n-uplet est une suite de n termes (n désigne un entier naturel), une liste de n éléments, dans un ordre précis.

La notion de n-uplet généralise celle de couple (on peut dire qu'un couple est un ). En pratique au lieu des mots 2-uplet, 3-uplet, 4-uplet, 5-uplet et 6-uplet, on utilise respectivement couple, triplet, quadruplet, quintuplet, et sextuplet.

On peut voir un n-uplet comme un mot composé de n lettres. Le n-uple formé des éléments a₁,a₂,...,a_n , pris dans cet ordre est noté (a₁,a₂,...,a_n).

Avec les éléments d'un ensemble à  p éléments on peut former  pⁿ  n-uples différents.

• Un n-uplet dont les éléments sont pris dans un ensemble E peut être vu comme un élément du produit cartésien  Ex Ex ... x E (n facteurs).

  Exemple. Un point de l'espace ⁿ  à n dimensions est souvent identifié au  n-uple (x₁,x₂,...,x_n) de ses coordonnées dans un repère cartésien donné.

• Un n-uple formé avec des éléments d'un ensemble E peut aussi être vu comme la donnée d'une application de l'ensemble {1,...,n} des n premiers nombres (entiers positifs) vers E.

  produit cartésien, paire, couple

retour à la liste

Les nombres entiers naturels  0, 1, 2, 3, 4, etc. servent à compter les éléments des ensembles finis.
L'ensemble des nombres entiers naturels se note . L'ensemble des nombres entiers naturels autres que 0 se note^* .

• En théorie des ensembles*, on définit les nombres entiers naturels (on dit aussi nombres naturels ou entiers naturels, ou, en abrégé, les naturels) comme les cardinaux des ensembles finis.
  0 est le cardinal de , l'ensemble vide,
  1 est le cardinal de l'ensemble {0} qui a 0 pour seul élément,
  2 est le cardinal de l'ensemble {0,1},
  3 est le cardinal de l'ensemble {0,1,2},
  etc.
  
  Grâce à des axiomes appropriés (par exemple, l'axiome du choix* et l'axiome de l'infini*), on prouve que les entiers naturels forment un ensemble, , qui est infini.

  L'addition, la multiplication dans ainsi que l'ordre usuel sont introduits à partir des opérations de même nom portant sur les cardinaux. En particulier :

  - Dans le cas où A et B sont des ensembles disjointsayant respectivement a et b éléments, la somme card(A)+card(B) est définie comme le cardinal de la réunion  AB.

  - Dans tous les cas, le produit card(A)xcard(B) est défini comme le cardinal du produit cartésien  AxB.

  L'ordre usuel des entiers naturels est défini à partir de la relation d'ordre entre cardinaux, ou bien par la propriété suivante :

  Étant donné deux entiers naturels  m et n, on a  m n ssi il existe un entier naturel  p tel que  n= m+ p .

• Le théorème suivant , très important, est très souvent utilisée (il est en effet équivalent au principe de récurrence : voir l' axiome A5 de Peano)

  Théorème du bon ordre naturel Tout ensemble non vide de nombres entiers naturels a un plus petit élément. Autrement dit , ordonné par , est bien ordonné*.

• Axiomes de Peano. G. Peano a défini l'ensemble des entiers naturels de manière axiomatique : on utilise les symboles et quantificateurs logiques, les signes, = de la théorie des ensembles, deux symboles nouveaux : 0 (zéro) et ⁺ ( n⁺ est appelé le successeur de n) et les axiomes suivants :

  A1   0 (zéro est un entier naturel)
  A2   nimplique n⁺ (tout entier naturel a un successeur qui est un entier naturel)
  A3   Si  m et  n sont des entiers naturels tels que m⁺ = n⁺ alors m= n (deux entiers naturels qui ont même successeur sont égaux)
  A4   Si net n0, alors il existe un entier mtel que m⁺= n (tout entier naturel positif a un prédécesseur)
  A5  (Axiome de récurrence). Si une partie P de contient 0 et si le successeur d'un élément quelconque de P appartient aussi à P, alors P=.

  récurrence

retour à la liste

Isaac Newton (25 décembre 1642 - 20 mars 1727) a dit de lui-même :

" Je me fais l'effet de n'avoir pas été autre chose qu'un garçon jouant sur le rivage, et m'amusant de temps à autre à trouver un caillou plus poli ou un coquillage plus joli qu'à l'ordinaire, tandis que le grand océan de la vérité se déroulait devant moi sans que je le connusse. "

Parmi les cailloux et les coquillages, Newton a découvert de nombreuses méthodes permettant de résoudre de manière approchée divers problèmes importants à son époque (et encore aujourd'hui) comme le calcul d'une surface limitée par une courbe, ou la résolution d'équations de la forme f(x) = 0.

La méthode de Newton consiste --- pour une équation de la forme f(x) = 0, avec x l'inconnue et f une fonction qui admet une dérivée (en tout point assez voisin de la solution cherchée) --- à interpréter la fonction f comme définissant une courbe dans un repère plan, et les solutions comme les abscisses des points d'intersection de cette courbe avec l'axe des abscisses ; à partir d'une valeur approchée x₁ choisie un peu au hasard, on calcule y₁ = f(x₁), puis x₂, abscisse du point d'intersection avec l'axe des abscisses de la tangente à la courbe représentative de f au point (x₁ ; y₁).

Sous certaines conditions, on a la garantie que x₂ est plus proche de la solution cherchée que x₁ et que si l'on recommence le procédé (avec x₂ à la place de x₁) on obtiendra peu à peu une suite (x_n) dont les termes se rapprochent de la solution cherchée.

Voir continue (fonction), fonction, graphe, limite (d'une fonction).

retour à la liste

Les jeux de Nim (ou jeux de NIM) se jouent avec de simples tas de cailloux (ou d'allumettes ...) : dans un tel jeu, deux joueurs jouent chacun à leur tour en prélèvant des cailloux dans certains tas et en formant éventuellement de nouveaux tas, conformément à des règles invariables qui sont les mêmes pour les deux joueurs. Ces règles font qu'au bout d'un certain temps, la partie s'arrête, l'un des joueurs ne pouvant plus jouer en respectant les règles : son adversaire est déclaré gagnant.

Un exemple typique de jeu de Nim est le jeu de Marienbad, connu par le film d'Alain Resnais "l'année dernière à Marienbad" où il est joué avec des allumettes. La règle est : chaque joueur à son tour choisit un tas et y prend autant d'allumettes qu'il veut (une au minimum); les allumettes prises sont retirées du jeu; le gagnant sera celui qui prélèvera la (ou les) dernière(s) allumette(s). Il est évident que la partie s'arrêtera, faute d'allumettes. Dans la version classique, 15 allumettes sont disposées au départ en 5 tas, comportant respectivement 1, 2, 3, 4, et 5 allumettes. Le joueur qui joue en premier est sûr de l'emporter s'il joue parfaitement. Dans la variante où on disposerait au départ de 4 tas comportant respectivement 1, 3, 5 et 7 allumettes, le premier joueur est sûr de perdre, à condition que le second joue parfaitement...

retour à la liste

On donne le nom de nombres à tous les êtres mathématiques que l'on peut combiner entre eux par des opérations telles que l'addition et la multiplication. On utilise des nombres pour mesurer des grandeurs, et pour combiner ensemble des grandeurs de même nature.

Depuis la plus haute Antiquité, les nombres ont exprimé l'idée de quantité et de mesure. Beaucoup de problèmes apparemment simples, car exprimés à l'aide d'opérations simples (addition et multiplication) portant sur des nombres simples (1,2,3,4,5,...), se sont avérés difficiles. Ces problèmes ont été de mieux en mieux compris grâce à l'invention et à la construction de nouveaux nombres : soumis aux mêmes opérations que les précédents, mais bien plus généraux, ces nouveaux nombres ont permis de trouver des méthodes de résolution :

Les principales sortes de nombres sont les entiers naturels, les entiers relatifs, les nombres décimaux, les nombres rationnels, les nombres réels, les nombres complexes.

Les nombres naturels 0,1,2,... permettent de compter des objets, bien distingués les uns des autres. Les nombres naturels sont une notion primitive des Mathématiques, introduite par des axiomes. Toutes les autres espèces de nombres peuvent être construites à partir des nombres naturels.

Les nombres entiers (relatifs) généralisent les nombres naturels en utilisant l'idée de signe (+ ou - ); permettent de graduer des échelles de mesure et de comparer les nombres naturels du point de vue de l'addition (usage de la soustraction, différences entre entiers naturels)

Les nombres décimaux permettent de mesurer les longueurs avec une précision aussi grande que voulue (usage de la virgule et des décimales)

Les nombres rationnels (ou fractionnaires) permettent et de comparer les nombres entiers du point de vue de la multiplication (usage de la division et des fractions, quotients de nombre entiers).

Les nombres réels généralisent tous les nombres précédents: de mesurer exactement les longueurs géométriques (avec une précision infinie) et d'exprimer l'idée de continité (usage des passage à la limite, et des fonctions continues). Ils permettent de décrire et d'étudier l'espace et le temps physiques et de les généraliser.

Les nombres complexes généralisent encore les nombres réels et permettent de résoudre, au moins de manière théorique, les équations algébriques à une seule inconnue. Par contre, ils ne peuvent pas être ordonnés de manière compatible avec les opérations usuelles, addition et multiplication.

retour à la liste

Une fonction est numérique si les valeurs qu'elle prend sont des nombres (souvent, des nombres réels).

Une " fonction numérique d'une variable réelle " est une fonction dont le graphe est inclus dans R x R.

retour à la liste

Une opération est une règle qui, à partir de deux éléments de même nature (deux nombres, deux ensembles, deux déplacements, deux fonctions, etc.) permet d'en définir un troisième.

D'une manière formelle , une opération dans un ensemble E est une fonction dont l'ensemble de départ est le produit cartésien ExE et dont l'ensemble d'arrivée est E. Lorsqu'une opération est partout définie (son ensemble de définition est ExE) , elle est souvent indiquée avec un signe particulier, par exemple *  : l'élément qui correspond à un couple (a,b) par l'opération * est noté a*b.

a*b est appelé le résultat de l'opération * sur les éléments a et b. Chacun des élément s   a, b   sont les facteurs (ou les termes) de l'expression a*b.

voir loi de composition.

retour à la liste

voir élément symétrique

retour à la liste

Relation permettant de comparer deux par deux certains éléments et de présenter ceux qui sont comparables dans un certain sens : de gauche à droite, de haut en bas, du clair au foncé, du petit au grand etc. Si tous les éléments d'un ensemble E peuvent être comparés deux à deux, la relation d'ordre est dite totale sur E. Dans le cas général, une relation d'ordre n'est que partielle : certains éléments ne peuvent être comparés.

Une relation binaire R dans un ensemble E est appelée une relation d'ordre dans E si elle vérifie les trois propriétés suivantes, appelés axiomes des relations d'ordre :

(O1) Réflexivité. Pour tout élément x de E , on a xRx.
(O2) Antisymétrie. Pour tout couple (a,b) d'éléments de E, on a l'implication (aRb et bRa) a=b
(O3) Transitivité. Pour tout triplet (a,b,c) d'éléments de E, on a l'implication (aRb et bRc) aRc

retour à la liste

Dans un graphe, ou dans un polyèdre, le nombre d'arêtes incidentes à un sommet (du graphe ou du polyèdre) est appelé le degré ou l'ordre de ce sommet.

retour à la liste

Terme primitif de la Logique mathématique : à partir de deux propositions, A et B, on peut former une nouvelle proposition qui s'écrit (A ou B). Cette proposition (A ou B) est vraie si (et seulement si) l'une au moins des propositions A et B est vraie.

Autrement dit, la proposition (A ou B) est vraie :
- si A est vraie (peu importe alors la vérité de B)
- si B est vraie (peu importe alors la vérité de A)

la proposition (A ou B) est fausse lorsque A et B sont fausses toutes les deux.

retour à la liste

Un ensemble de points est ouvert si tous ses éléments sont intérieurs à cet ensemble. De manière imagée, un ensemble ouvert doit contenir autour de chacun de ses points "un nuage de valeurs approchées". C'est la Topologie qui fournit un cadre approprié pour des définitions générales et rigoureuses de ces idées.

En géométrie on parle de segments ouverts, de disques ouverts , de demi-droites, de demi-plan, de demi-espace, etc. , ouverts : les points de ces ensembles leur sont intérieurs. On parle d'intervalles ouverts dans les ensembles ordonnés.

Ouverts de: un ensemble X de nombres réels est dit ouvert si dès qu'il contient un nombre x, il existe deux nombres x' et x" tels que l' intervalle ouvert ]x',x"[ contienne x et soit contenu dans X. Un ensemble de nombre réels est dit fermé si l'ensemble complémentaire -E est ouvert. Ainsi, l
L'intervalle [0,1[ de n'est ni ouvert ni fermé dans . L'ensemble des nombres rationnels n'est ni ouvert ni fermé dans .

Ouverts du plan : un ensemble X de points du plan est dit ouvert si dès qu'il contient un point P, il existe un réel r>0 tels que tout point M vérifiant PM < r appartienne à X. (L'ensemble des points M vérifiant PM < r est le disque ouvert de centre P et de rayon r).

Ouverts d'un espace métrique. La définition précédente se généralise facilement. Dans un espace E muni d'une distance d, un ensemble X de points de E est dit ouvert si dès qu'il contient un point p, il contient une boule ouverte de centre P (autrement dit il existe un réel r > 0 , dépendant de p, tel que tout point m vérifiant d(p,m) < r appartienne à X).

Ouverts topologiques. La Topologie généralise très largement les notions précédentes. Les ensembles ouverts, en abrégé "les ouverts", sont définis de façon indirecte, par les propriétés ensemblistes qu'il doivent posséder. Ces propriétés sont prise pour axiomes des espaces topologiques*

Axiomes des ensembles ouverts. Un ensemble E devient un espace topologique, que l'on note (E,), ou simplement E si le contexte est suffisamment clair, dès que l'on se donne une collection de parties de E, appelées les ouverts de l'espace topologique E, avec les propriétés suivantes :

• (O₀)   et E appartiennent à .
• (O₁)     Toute réunion d'ensembles appartenant à appartient à .
• (O₂)     Toute intersection d'un nombre fini d'ensembles appartenant à appartient à .

Les parties complémentaires des ensembles ouverts sont appelés les ensembles fermés ou "les fermés" de E.

fermé

retour à la liste

Les ensembles de la forme ] a, b[ , s'appellent les intervalles ouverts de E.

fermé

retour à la liste

Remarque. Si on ne retire au segment [AB] que le point B on obtient un segment dit semi-ouvert noté [AB[ (oralement, on parle du «segment A B , fermé en A et ouvert en B»).

Remarque. Un segment ouvert ]AB[ est un ensemble ouvert de la droite (AB) vue comme espace topologique* mais n'est ni ouvert ni fermé pour la topologie usuelle du plan (sauf dans le cas très particulier où A=B, auquel cas ]AB[ est vide).

fermé

retour à la liste

Une paire est la donnée de deux éléments, sans ordre particulier (à la différence d'un couple qui associe deux éléments dans un ordre précis).

• Sauf indication contraire, les éléments d'une paire sont différents : une paire est donc un ensemble à deux éléments.
• Avec les éléments d'un ensemble à  n éléments on peut former   paires différentes.

retour à la liste

Géométrie plane.
Deux droites sont parallèles si elles sont confondues ou si elles n'ont aucun point commun.
Lorsque (D) et (D') sont parallèles, on dit aussi que (D) est parallèle à (D'), ou que que (D') est parallèle à (D).
Une droite parallèle à une droite donnée D est appelée une parallèle à D.

	5ème postulat d'Euclide : postulat des parallèles (géométrie euclidienne plane).
	Par un point pris hors d'une droite, il passe une parallèle à cette droite et une seule.
	(géométrie euclidienne plane)
	Deux droites parallèles à une même troisième sont parallèles entre elles ; autrement dit, la relation de parallélisme est transitive. Il en résulte que la relation "être parallèle à" est une relation d'équivalence entre droites. On dit de droites parallèles qu'elles ont la même direction.

Géométrie dans l'espace.
Deux droites sont parallèles si elles sont dans un même plan et sont parallèles dans ce plan.
Deux plans sont parallèles si ils sont confondus, ou si ils n'ont aucun point commun.

Géométries quelconques : deux droites sont parallèles si elles sont confondus ou si elles n'ont aucun point commun tout en étant dans un même plan.

Espaces affines* de dimension* quelconque*.
Deux sous-espaces* de dimension* k sont parallèles si ils sont confondus, ou si ils n'ont aucun point commun tout en étant dans un même sous-espace de dimension k+1.

• Deux sous-espaces affines sont parallèles ssi ils ont le même sous-espace vectoriel associé*.

  relation d'équivalence, axiome, géométries euclidiennes, non euclidiennes

retour à la liste

Quadrilatère ayant ses cotés opposés parallèles deux à deux (Figure de la géométrie euclidienne plane).

	Pour un quadrilatère ABCD non croisé du plan les propriétés suivantes sont équivalentes
	(1) ABCD est un parallélogramme (2) Le quadrilatère admet deux cotés opposés qui sont parallèles, de même longueur. (3) Les diagonales [AC] et [BD] se coupent en leur milieu. (4) Le quadrilatère ABCD a un centre de symétrie.
	Pour un quadrilatère général, les propriétés (1), (3), (4) et (2')sont encore équivalentes, avec : (2') Le quadrilatère admet deux cotés opposés qui sont parallèles, de même longueur et de sens contraire.

retour à la liste

Un ensemble F dont tous les éléments appartiennent aussi à un ensemble E, c'est à dire qui est inclus dans E, est appelé une partie de E, ou un sous-ensemble de E.

L'ensemble vide, , a une seule partie : lui-même. Tout ensemble non vide E contient deux parties remarquables : l'ensemble vide, et l'ensemble E lui-même(parfois appelé partie pleine de E). Une partie propre de E est une partie de E qui est différente de E.

• Comme l'affirme un des axiomes de la théorie des ensembles, les parties d'un ensemble E forment un nouvel ensemble, noté P(E) ou ( E) , ou encore 2^E .
• Un autre axiome de la théorie des ensembles affirme que si on se donne un ensemble E et une propriété P( x) , les éléments x de E qui possèdent la propriété P forment une partie de E donc un nouvel ensemble. Cette partie est introduite par l'écriture :
  { xE P( x) } ou encore { xE; P( x) }

• Cantor a montré que tout ensemble avait "plus" de parties que d'éléments (d'où il résulte en particulier qu'il n'y a pas un seul " infini ", mais une infinité ! Voir cardinaux infinis).

  	(G. Cantor)
  	Quelque soit l'ensemble E, il n'existe aucune surjection de E sur P(E).

  La démonstration, par l'absurde, est à la fois simple et instructive.

  Supposons qu'une telle surjection f existe.
  La partie  C de E définie par  C={ xE; xf( x) } est alors l'image par f d'un élément c de E : C=f(c).
  Mais chacune des éventualités cC ou  cC conduit à une contradiction :
  - si  cC , alors  cf( c), par définition de C, d'où cC, puisque C=f(c).
  - si cC , on a cf( c), puisque C=f(c), donc  cC, par définition de C.

  inclus, vide

retour à la liste

retour à la liste

Une application bijective d'un ensemble E sur lui-même est appelée une permutation de E.

retour à la liste

Le plan est l'espace de la géométrie euclidienne plane.

Plus généralement, en géométrie dans l'espace, un plan est une partie de l'espace qui a les propriétés du plan.

Le mot plan est un terme primitif de la géométrie dans l'espace

retour à la liste

Une figure géométrique est dite plane si tous les points qui la constituent sont sur un même plan.

retour à la liste

Une figure de géométrie plane est dite plate si tous les points qui la constituent sont sur une même droite.

Une figure de géométrie dans l'espace est dite plate si tous les points qui la constituent sont sur une même plan.

Une figure de géométrie dans un espace à n dimensions * est dite plate si tous les points qui la constituent sont dans un même sous-espace* à n-1 dimensions*.

retour à la liste

Terme primitif de la géométrie. qui traduit l'idée d'endroit précis, de lieu sans aucune étendue.

Le plan, l'espace, et plus généralement tout espace géométrique peut être pensé comme un ensemble de points : chaque objet géométrique peut alors être vu comme un sous-ensemble de points avec des propriétés particulières.

Dans le plan ou dans l'espace, un point est parfaitement déterminés par deux droites distinctes qui passent par ce point.

retour à la liste

[D'origine grecque : "poly"-"èdre" = "plusieurs"-"faces".]

Découpons des polygones plans et assemblons les dans l'espace de manière à ce que chacun des cotés des polygones se retrouve comme coté commun à exactement deux polygones. L'assemblage final forme une surface (sans bord) appelée surface polyédrique ou polyèdre.

Les surfaces des polygones utilisés sont les faces du polyèdre. Leurs cotés constituent les arêtes du polyèdre et leurs sommets sont les sommets du polyèdre.

On donne aussi le nom de polyèdre à la portion d'espace délimitée par une surface polyédrique.

On classe souvent les polyèdres suivant leur nombre de faces : un tétraèdre a 4 faces, un hexaèdre (par exemple un cube ) en a 6, un octaèdre, 8, un dodécaèdre, 12, un icosaèdre, 20.

• Un polyèdre est régulier quand tous ses sommets, toutes ses arêtes et toutes ses faces jouent le même rôle . Plus précisément, si on se donne deux triplets (s,a,f) et (s',a',f') tels que :
  -  f est une face, a est une arête de f, s un sommet de a.
  -  f' est une face, a' est une arête de f', s' un sommet de a'.
  alors, il existe toujours un déplacement de l'espace tout entier qui amène s en s', a en a', f en f'.

Le mot polyèdre s'emploi dans la pratique avec plusieurs degrés de généralité : des polyèdres divers possédant des propriétés similaires sont considérés comme un seul polyèdre
- polyèdres géométriques : des polyèdres qui ne diffèrent que par leur taille et leur diposition dans l'espace peuvent être considérés comme un seul polyèdre. On dira ainsi le cube ou le tétraèdre régulier.

• Dans l'espace, il n'y a en tout et pour tout que 5 polyèdres régulier convexes.

- polyèdres combinatoires : des polyèdres qui ne diffèrent que par la forme de leurs faces mais qui ont la même recette d'assemblage peuvent être considérés comme un seul polyèdre. On dira par exemple qu'il y a, pour chaque entier n, une seule pyramide à n faces ( le tétraèdre pour n=4)

retour à la liste

Ligne brisée fermée, composée de plusieurs segments mis bout à bout. Le nom vient du grec "poly" (plusieurs) et "gonos" (coté). Un polygone est un exemple particulier de courbe fermée.

Un polygone est une figure géométrique formée par  n points A₁, A₂,Š, A_n (les sommets du polygone), et les n segments A₁A₂ , A₂A₃ , Š , A_n-1A_n , A_nA₁ (les cotés du polygone). Les angles formés par deux cotés consécutifs, c'est à dire les angles

sont appelés les angles du polygone. Un polygone à  n cotés (n3) est aussi appelé un n-gone. Sauf précision contraire, un polygone est plan : tous ses sommets sont dans un même plan.

• Deux sommets (ou deux cotés) consécutifs d'un polygone sont dit adjacents. Dans l'usage le plus courant, un polygone est simple : deux cotés non consécutifs ne se rencontrent pas et deux cotés consécutifs n'ont en commun que l'un de leur sommets.
  Un polygone P est croisé si deux de ses cotés, non consécutifs et non parallèles, se rencontrent en un point qui n'est pas un sommet de P.
  Par abus de langage, on dit souvent polygone non croisé au lieu de polygone simple et un polygone qui n'est pas simple est souvent appelé polygone croisé. (Un polygone simple est toujours non croisé, mais on construit facilement des polygones qui ne sont ni simples ni croisés).
  
• Le bord d'un polygone est l'ensemble des points qui appartiennent à ses cotés.

  	(de Jordan)
  	Le bord d'un polygone simple du plan sépare le plan en deux régions dont une seule (appelée l'intérieur) est bornée.

  Dans l'usage courant, le mot "polygone" désigne aussi bien un polygone simple que son bord ou que la surface qu'il détermine (formée des points intérieurs ou sur le bord). Par exemple, un polygone est dit convexe lorsque sa surface est convexe.

• Pour de nombreuses valeurs de n, les n-gones ont des noms particuliers formés avec le suffixe "-angle", "-gone" ou "&endash;latère" (en latin "côté") et un préfixe d'origine grecque ou latine qui indique le nombre de cotés:
  triangle : 3, quadrangle ou quadrilatère : 4, pentagone : 5, hexagone : 6, heptagone : 7, octogone : 8, ennéagone : 9, décagone : 10, endécagone : 11, dodécagone : 12, icosagone : 20, myriagone : 1000.]
• Un polygone est régulier quand on peut, en faisant tourner la figure d'un angle convenable autour d'un certain point fixe, amener simultanément chaque sommet à coïncider avec son suivant. Le point autour duquel on a fait tourner la figure s'appelle le centre du polygone régulier. Autrement dit un polygone est régulier s'il existe une rotation qui transforme chacun de ses sommets en son suivant.

  Un polygone est régulier ssi ses côtés sont tous de même longueur et ses angles tous égaux.

  Le terme "polygone régulier" s'applique à des polygones simples (c'est l'usage le plus courant) aussi bien qu'à des polygones croisés.
  Un polygone régulier croisé est dit " étoilé " : on parlera par exemple du pentagone régulier étoilé ("pentagramme" dans la tradition symbolique) ; remarquons que le dessin usuel d'une étoile régulière à 5 branches est en réalité un polygone à dix cotés dont les angles sont alternativement rentrants et saillants.

• Quand les sommets d'un polygone sont pris dans l'espace, sans être nécessairement dans le même plan, on parle de polygone gauche.
  

retour à la liste

En combinant des nombres et des variables représentant des nombres à l'aide des opérations addition et multiplication, on obtient des expressions algébriques appelées polynômes. Les polynômes peuvent à leur tour être combinés entre eux par addition et multiplication.
Remarque. Dans l'écriture des polynômes, des signes de soustraction ( - ), de division (barres de fraction, / ou ^__) ou des exposants peuvent apparaître : ces signes ne sont que des commodités d'écriture : les variables d'un polynôme n'apparaissent jamais ni dans un dénominateur ni dans un exposant.

Exemples. 1 + 2 x⁵ ,   2 + x +  yx z+(-4) ,   ( a+ b)² sont des écritures de polynômes, mais 2^x, x/y , x^y n'en sont pas.

Malgré la présence du signe " - " , l'expression est l'écriture d'un polynôme, c'est la forme simplifiée de. De même, et sont des écritures de polynômes : ce sont des simplifications dex rx r et de.

L'usage des polynômes permet d'ordonner les calculs avec des nombres et d'établir des propriétés remarquables concernant les nombres. Les polynômes d'une ou de plusieurs variables réelles sont beaucoup utilisés pour calculer les fonctions de manière approchée (voir développements limités*, développements en série*,..).

Lorsque les nombres concernés sont pris dans un ensemble donné de nombres K (un anneau un corps), les expressions obtenues représentent des polynômes sur K  (Notation. L'ensemble des polynômes sur K avec les variables X,Y,Z est noté K[X,Y,Z]) :

Pour l'écriture des polynômes, on adopte des règles de remplacement et de simplification qui imitent (en les généralisant) les propriétés usuelles de l'addition et de la multiplication entre nombres. Deux expressions algébriques différentes mais qui peuvent être identifiées en vertu des propriétés générales de l'addition et de la multiplication des nombres de K (présence d'éléments neutres, associativité ou commutativité des opérations, distributivité de la multiplication par rapport à l'addition) ; voir anneau, corps)) doivent alors être considérés comme un seul et même polynôme.

Exemple : (x+1)² et x²+2x+1 sont des écritures équivalentes et représentent donc un seul polynôme de  ainsi (x+1)²=x²+2x+1

De même

1.x = x
x - x = 0 (polynome nul)
x + 3x = 4x
(a+b)² = a²+2ab+b² (polynome de)

Pour l'étude générale des polynômes, il est commode de représenter aussi certains nombres par des lettres. Pour éviter de les confondre avec les variables, on leur donne un nom différent : on parle de coefficients, de paramètres ou de constantes. Pour les variables on utilise souvent les lettres x, y, z, ... (ou X, Y, Z, ...) pour les paramètres ou les constantes, les lettres a, b, c ou m, p, q, r, ...

Par exemple, peut-être vu comme un polynôme en la variable x: les lettres a, b, c sont alors vues non comme des variables mais comme des constantes ou des paramètres : les expressions et ne sont que des écritures de nombres.

Autre exemple : dans l'expression de l'aire d'un cercle de rayon r, la lettre est une constante, la lettre r une variable.

(Cette même entrée " polynôme " était plus détaillée dans la version 1995 du glossaire parue dans les actes MATh.en.JEANS sous forme "papier". Elle devrait être bientôt disponible sur ce site.)

retour à la liste

syn. axiome.

retour à la liste

« Par un point pris hors d'une droite (D), il passe une droite parallèle à (D) et une seule.»

retour à la liste

syn. début de mot.

retour à la liste

Nombres premiers qui apparaissent dans l'écriture d'un nombre entier sous forme de produit. Tout nombre entier supérieur à 1 est le produit de facteurs premiers.

Exemple. 1996 s'écrit 2x2x499 et a deux facteurs premiers : 2 et 499.

Plus généralement on a le théorème suivant, considéré comme le théorème fondamental de l'Arithmétique.

Tout nombre entier n > 1 s'écrit sous la forme n = aa x bb x cg x ... x dd où a, b, c, ..., d sont les facteurs premiers de n et où a, b, g, ..., d sont des entiers positifs ; de plus, cette écriture, appelée décomposition de n en facteurs premiers, est unique, à l'ordre près des facteurs a, b, c, ..., d .

Exemples : les facteurs premiers de 30 sont 2 , 3 et 5 car la décomposition de 30 est 30 = 2 x 3 x 5 ; ceux de 12 sont  2 et 3 car 12 = 2 x 2 x 3 = 2² x 3.

retour à la liste

Certains nombres entiers, autres que 0 ou 1, s'avèrent impossibles à partager en plusieurs parts égales autrement qu'en mettant une seule unité dans chaque part. Ce sont les nombres premiers.

Exemples :

Les nombres  2, 3, 5, 7, 11, 13, 17, 19, ... sont premiers,
Les nombres 4 = 2x2, 6 =2x3, 8 = 2 x 2 x 2 , 9=3 x 3, 10 = 2 x 5, 12 = 2x2x3, ... ne sont pas premiers.

Les nombres premiers sont intéressants parce qu'ils permettent de fabriquer tous les autres nombres (0 et 1 exceptés) à l'aide de la multiplication. Par exemple :

Nombre premier : nombre entier naturel différent de 0 et de 1, qui n'est pas le produit de nombres naturels plus petits que lui. Un nombre non premier, autre que 0 et que 1, est appelé nombre composé.
Remarque : un nombre est premier s'il n'est divisible que par 1 et par lui-même.

[Euclide] Il existe une infinité de nombres premiers.

Liste des 1000 premiers nombres premiers.

Si un nombre premier divise un produit de nombres entiers, il divise alors au moins l'un de ces nombres.

Ce dernier théorème permet d'étendre la notion de " nombre premier " pour des ensembles de nombres plus généraux ( anneaux* de nombres).

premier (facteur), diviseur

retour à la liste

Des nombres entiers a, b, ... , c sont dit premiers entre eux si 1 est le seul entier positif qui les divise tous.

Par exemple 12 et 25 sont premiers entre eux ainsi que 6, 10 et 15. On distinguera le cas des nombres 12, 25, 77 qui sont premiers entre eux deux à deux, donc aussi premiers entre eux dans leur ensemble, du cas des nombres 6, 10, 15, qui sont premiers entre eux dans leur ensemble mais pas deux à deux (2 divise 6 et 10, 5 divise 10 et 15, 3 divise 6 et 15, mais 1 est le seul à pouvoir diviser à la fois 6, 10 et 15).

Le théorème de Bézout [Etienne Bézout, mathématicien français, né près de Fontainebleau, 1730-1783] caractérise la propriété pour deux nombres d'être premiers entre eux par une équation :

	[Théorème de Bézout]
	Deux entiers a et b sont premiers entre eux ssi il existe deux entiers (positifs ou non) u et v tels que ua+ vb= 1 (autrement dit : l'équation ua+ vb= 1, où les inconnues sont  uet v a au moins une solution en nombres entiers).

Exemple. 12 et 25 sont premiers entre eux : (-2) x 12 + 1 x 25 = 1 et l'équation ux12 + vx25= 1  a bien au moins la solution  (-2, 1)  en nombres entiers.

	Cette caractérisation est générale : des entiers a, b, c, ... sont premiers entre eux ssi l'équation ua + vb+ wc+ ... = 1 a au moins une solution (u, v, w, ...) en nombres entiers.
	On peut ainsi reconnaître d'une autre façon que les trois entiers 6, 10, 15 sont premiers entre eux : l'équation 6u+ 10v+ 15w = 1 admet la solution (1, 1, -1) vu que 6x1 + 10x1 + 15x(-1) = 6 + 10 - 15 = 1.

retour à la liste

En mathématiques l'activité de preuve consiste à expliquer comment un certain énoncé, appelé conclusion, est démontré, c'est à dire est déduit logiquement d'autres énoncés, appelés hypothèses. Les explications doivent pouvoir être vérifiées, elles sont donc généralement présentées par écrit : le texte prend le nom de preuve mathématique.

retour à la liste

Mot désignant un objet mathématique de base, un objet qui n'est pas construit à partir d' objets plus simples. Les termes primitifs servent de point de départ aux raisonnements et aux théories mathématiques.

Dans un dictionnaire usuel, la définition des mots fait appel à d'autres mots, qui eux-mêmes renvoient à d'autres mots, etc. : on finit par tourner en rond, les définitions "bouclent". En mathématiques, on évite ce phénomène de référence circulaire : sauf exception , tous les mots avec lesquels on veut faire des raisonnements doivent pouvoir être définis à partir de mots plus simples. Les exceptions sont des mots de base définis une fois pour toute avant les autres et sont appelées termes primitifs. Les objets mathématiques correspondants sont appelés objets primitifs.

Comment fait-on pour introduire, pour "définir" des objets et des termes primitifs ? Réponse : on définit un objet primitif de manière indirecte en donnant une liste de propriétés que cet objet doit vérifier : ces propriétés, vraies par convention , servent de règles de base et sont appelées axiomes.
Ce procédé de défintion pour les termes et les objets primitifs est appelé la définition axiomatique. (méthode axiomatique)

Tout domaine mathématique particulier, toute théorie mathématique, peut être construit de cette manière à partir d'une liste de termes primitifs et d' axiomes. Ces termes et règles de base, permettent, avec les règles de la Logique mathématique, de construire de nouveaux objets, de définir de nouveaux termes, d'énoncer de nouvelles propriétés.

Termes et objets non primitifs sont appelés termes et objets dérivés.

Exemple 1 : une théorie des meubles Si on voulait faire une théorie mathématique des "meubles de maison", une théorie que parlerait de tables, de chaises, etc. ,
on commencerait par donner - une liste de termes primitifs , par exemple "meuble", "pied", "dossier", "grand", "moyen", "avec" - une liste d' axiomes , par exemple : Si un objet A (meuble, pied ou dossier) est avec un objet B, alors l'objet B est avec l'objet A .. Si un objet A (meuble, pied ou dossier) est avec un objet B, alors A et B sont différents. Un objet A (meuble, pied ou dossier) est grand ou moyen. Tout meuble est avec au moins 3 pieds. Tout pied est avec un meuble et un seul. Tout dossier est avec un meuble et un seul. Aucun meuble n'est avec un meuble Un pied est grand ou moyen. ...	Cela permettrait de définir des termes dérivés : Si un meuble M est avec un pied P, on dit que M a le pied P.et que P est un pied de M . Deux pieds P et Q sont dit de même taille si P et Q sont grands ou si P et Q sont moyens ou si P et Q sont petits. "sans" signifie "non avec", On appelle "bon meuble" un meuble ayant au moins 3 pieds et dont les pieds sont de même taille. On appelle "table" un bon meuble sans dossier . On appelle "chaise" un bon meuble avec un seul dossier et avec des pieds moyens. On appelle "tabouret" un bon meuble sans dossier avec des pieds moyens, etc.
Exemple 2 : La logique mathématique La Logique mathématique a elle aussi besoin de termes et d'objets primitifs. Si on choisit, par exemple, les mots "vrai", "non", "ou", "proposition", "démonstration", ... comme termes primitifs, on pourra, grâce à une liste de règles de base (les axiomes de la Logique) définir d'autres termes importants tels que "faux", "implique", "et", "équivalent", "axiome", "théorème", ...
Exemple 3. La géométrie (euclidienne) plane. Les axiomes de la géométrie plane précisent le sens et l'emploi de termes primitifs comme "point", "droite", "appartenance d'un point à une droite", "point entre deux autres", "angle", "longueur", "superposable" ... . Ils fournissent des règles de base ("deux points différents appartiennent à une droite et une seule" ; "si 3 points appartiennent à une même droite, l'un deux est entre les deux autres", règles sur le report de longueur et le report d'angle, etc.). Les mots "parallèle", "segment", "triangle", "carré", "losange", "hauteur", etc. , sont des termes dérivés.

définition, axiome , méthode axiomatique, théorie

retour à la liste

Résultat d'une multiplication ou expression de ce résultat sous forme multiplicative (c'est à dire utilisant une multiplication, éventuellement plusieurs fois). Il s'agit le plus souvent de nombres, mais on parle aussi de produit d'ensembles, de fonctions, de polynômes, de matrices, de vecteurs, etc.

Le produit de deux éléments a et b se note  ax b ou a.b (ou aussi  ab s'il n'y a pas de risque de confusion). Si la multiplication est associative, le produit de plusieurs nombres se note sans mettre de parenthèses :

Chaque nombre intervenant dans l'écriture d'un tel produit s'appelle un facteur. Ces nombres sont des diviseurs du nombre produit. Si la multiplication n'est pas commutative, on fera attention à l'ordre des facteurs dans l'écriture d'un produit.

Exemples.

25 est le produit de 5 et de 5.
Le nombre 15 se met sous la forme du produit 3x5.
Si  a et  b sont des nombres, l'expression  a²- b², représente le même nombre que le produit ( a+ b)( a- b)

produit de deux entiers naturels. Si A est un ensemble à a éléments et si B est un ensemble à b éléments, le produit ax b est, par définition, le nombre d'éléments du produit cartésien  Ax B.

multiplication, premier (facteur), diviseur

retour à la liste

voir cartésien (produit -)

retour à la liste

voir continu (puissance).

retour à la liste

La puissance d'un ensemble infini est son cardinal.

retour à la liste

La n-ième puissance d'un nombre a est le produit a x a x ... x a de n facteurs égaux à a.

retour à la liste

Quelques belles démonstrations illustrées du théorème de Pythagore : Le théorême de l'hypothénuse dit de Pythagore [pdf 60Ko] par Paul Gérardin, (Univ. Paris 6) , février 2006.

retour à la liste

adj. Qui se rapporte à des formules algébriques du second degré.

retour à la liste

Les résidus quadratiques d'un nombre entier positif n sont les restes de la division par n des carrés parfaits autres que 0.

Les résidus quadratiques des nombres premiers ont des propriétés particulières : ces propriétés peuvent être utilisés pour tester si un nombre est premier ou non (l'idée de départ étant qu'un nombre impair n est composé ssi il est la différence de deux carrés parfaits).

Plus formellement, r est résidu quadratique de n (on dit aussi que a est un résidu quadratique modulo n), si r<n et s'il existe deux entiers x et q tels que x² = nq+r.

Exemple : 3 est un résidu quadratique modulo 11 puisque c'est le reste de la division de 25 (carré parfait non nul) par 11 :   25 = 11x2+3.

retour à la liste

Polygone à 4 cotés.

retour à la liste

Figure géométrique formé de 4 points différents (appelés les points de base ou les sommets du quadrilatère) et des 6 droites qui joignent ces points deux à deux. Pour qu'une telle figure ne soit pas "dégénérée", il faut supposer que les 6 droites sont toutes différentes.

• A la différence d'un quadrilatère usuel, les 6 droites d'un quadrilatère complet jouent le même rôle : il n'y a pas de "diagonales".
• Dans le plan, les 6 droites d'un quadrilatère complet déterminent 7 points d'intersection, pourvu qu'aucune relation de parallélisme n'apparaîsse entre les droites.

retour à la liste

Résultat d'une division.

retour à la liste

Un nombre pour lequel le calcul de ce polynôme donne 0 quand on remplace la variable x du polynôme par ce nombre. " racine de P " (on dit aussi " zéro de P ") est synonyme de " solution de l'équation P(x) = 0 "..

retour à la liste

Nombre qui s'exprime sous forme de fraction a/b avec a et b entiers.

Dans l'Antiquité, le nombre exprimait généralement la longueur d'un segment, ce qui imposait d'avoir toujours une longueur de référence, qui servait à mesurer les autres longueurs. Avec des constructions géométriques simples, on pouvait alors ajouter des nombres, les soustraire, les multiplier ou les diviser, en faisant en fait ces opérations sur les segments. Se pose alors le problème de trouver la longueur d'un segment exprimée avec le segment de référence, dont la longueur est la " longueur unité ". Ce n'est pas toujours possible !

Exemple célèbre : on construit un carré sur le segment de référence, qui est ainsi le côté du carré ; la diagonale de ce carré pose problème. Sa longueur ne s'exprime pas comme multiple entier de la longueur unité, ni même comme fraction c'est-à-dire un multiple d'une sous-unité.

Depuis les Grecs, on classe les nombres réels en deux familles : les rationnels et les irrationnels. Les rationnels sont ceux qu'on peut exprimer comme fraction de la longueur unité (fraction de 1, donc sous la forme fractionnaire a/b avec a et b entiers) ; les irrationnels sont ... les autres.

L'ensemble des nombres rationnels se note. On peut y faire addition et multiplication avec de bonnes propriétés, permettant par exemple de résoudre toutes les équations polynomiales du premier degré.

La diagonale du carré de côté 1 est de longueur , doncest un irrationnel. On pourra essayer d'en donner un développement décimal illimité, par exemple, mais on ne pourra pas l'exprimer sous forme d'une fraction de deux nombres entiers.

On peut faire une construction de Q en considérant un rationnel comme un ensemble de fractions équivalentes (deux fractions sont équivalentes si " le produit des moyens est égal au produit des extrêmes ") ; cette construction a l'avantage de pouvoir se généraliser à d'autres ensembles pour lesquels on dispose d'une addition et d'une multiplication (l'ensemble des polynômes à coefficients dans R, par exemple).

majorant, minorant, réel.

retour à la liste

Quadrilatère plan ayant 4 angles droits (Figure de la géométrie euclidienne plane).

	Pour un quadrilatère ABCD non croisé du plan les propriétés suivantes sont équivalentes
	(1) ABCD est un rectangle (2) Le quadrilatère ABCD a 3 angles droits. (3) ABCD est un parallélogramme et ses diagonales, AC et BD, sont de même longueur. (4) ABCD est un parallélogramme ayant un angle droit.

retour à la liste

retour à la liste

Notion mathématique qui nous permet à la fois de calculer et de se repérer de manière précise dans l'espace et dans le temps; ces nombres servent notamment à mesurer des distances.

Les nombres réels sont à la fois utilisés en Algèbre, en Géométrie et en Analyse :

• Ce sont des nombres, qui généralisent les nombres entiers, les nombres décimaux et les nombres rationnels et qui, comme eux, peuvent être additionnés, multipliés et ordonnés avec de bonne propriétés (les nombres réels forment un *corps ordonné, archimédien et complet*) .
• Il y a une correspondance parfaite entre les nombre réels et les points d'une droite géométrique, ce qui permet de repérer un point par des nombres (coordonnées cartésiennes).
• Les *fonctions d'une ou de plusieurs variables réelles*(celles qui utilise des nombres réels comme variables dans leur définition) sont couramment étudiées pour décrire des relations géométriques (longueur d'une courbe, aire d'une figure, sinus d'un angle, etc.) ou l'évolution d'un phénomène physique au cours du temps (mouvement d'une masse ponctuelle, croissance d'une plante, température ou pression d'un gaz , intensité d'un courant, etc.).

L'ensemble des nombres réels se note . On classe souvent les nombres réels en deux familles : les rationnels et les irrationnels. (voir nombres rationnels)

On démontre la propriété fondamentale suivante de , qui n'est pas vraie pour l'ensemble des nombres rationnels :

[Théorème des coupures de Dedékind] Si A et B sont des parties disjointes de et si A est situé "avant" B, alors il existe un nombre réel "entre" A et B. Autrement dit, l'hypothèse que tout nombre de A est inférieur à tout nombre de B garantie l'existence d'un nombre supérieur à tout élément de A et inférieur à tout élément de B (il majore strictement A et minore strictement B).

Dans la pratique courante, on s'intéresse à la situation où A et B forment une coupure* (au sens de Dedekind), c'est à dire lorsqu'un seul nombre réel se trouve entre A et B et on donne des valeurs approchées de ce réel en utilisant des éléments de A ou des éléments de B.

On peut illustrer cette " pratique courante " avec la méthode utilisée par Archimède pour calculer le nombre . Pour un cercle de diamètre 1, on cherche la longueur de la circonférence (et on obtiendra donc une valeur depuisque cette longueur vautx diamètre).

Archimède considère deux ensembles de polygones réguliers, certains inscrits dans le cercle, les autres circonscrits au cercle ; les longueurs de ces polygones forment aussi deux ensembles de nombres, les uns sont tous avant la longueur de la circonférence, les autres sont tous après elle ; le nombre réel "circonférence du cercle" est ainsi coincé entre ces deux ensembles de nombres, et on en obtiendra un encadrement en prenant une longueur de polygone inscrit et une longueur de polygone circonscrit, pour peu qu'on réussisse à les calculer avec suffisamment de précision.

[Archimède obtint : 3 + 10/71 << 3 + 10/70.]

majorant, minorant, rationnel.

retour à la liste

retour à la liste

Certaines figures partagent un espace donné en plusieurs régions (on utilise aussi parfois le mot zone)

Dans la langue usuelle, ce terme n'est pas bien défini : il existe une petite région appelée "France" (celle de Roissy-en-France), qui se trouve dans la Région "Ile-de-France", laquelle se trouve en "France" ! En mathématiques, c'est le plus souvent un ensemble de points délimité (dans le plan ou dans l'espace) par des droites ou des plans, par des courbes ou par des surfaces. La façon dont la région est délimitée est alors précisée. Deux droites sécantes du plan y déterminent quatre régions. (Combien de régions sont déterminées par les plans des faces d'un cube ?).

Remarque. "Région" peut aussi se comprendre dans le sens de "voisinage" : ce ne sont justement pas les limites de la région qui seront intéressantes, mais le fait qu'on puisse être assez proche d'un point, d'une figure. Comme dans la vie courante, on peut s'intéresser à une région autour d'un point, d'une ligne (les rives du Nil forment une région fertile ; mais quelle serait la définition précise de "rive" du Nil ?). A titre d'exemples d'utilisation de ce vocabulaire, voir continue (fonction), face (d'un polyèdre).

On utilise l'expression "région délimitée par" ou "zone définie par" pour parler d'une partie d'espace constituée de tous les points qui, par rapport à une (ou plusieurs) figure donnée, sont situés de la même manière. Dans le plan, l'intérieur et l'extérieur d'un triangle sont les deux régions délimitées par ce triangle. Plus généralement, certaines lignes ont la propriété de partager le plan en "régions" : les droites (voir demi-plan), les polygones non croisés, les courbes fermées de Jordan . De même certaines surfaces (fermées) partagent l'espace en régions. Comme les figures, les régions sont considérés comme des ensembles de points, mais leur définition précise dépend des propriétés de l'espace étudié et des figures qui définissent ces régions. La Topologie donne un procédé général rigoureux de définition : les régions délimitées par des figures sont les composantes connexes* de l'ensemble obtenu en enlevant à l'espace tous les points qui appartiennent à l'une des figures considérées.

retour à la liste

retour à la liste

La réunion (ou union) de deux ensembles A et B est l'ensemble formé des éléments qui appartiennent à A ou à B. On le note AB (lire «A union B»).

La réunion de plusieurs ensembles A, B, C, ...  est l'ensemble formé des éléments qui appartiennent à l'un au moins des ensembles A, B, C, ...

• En théorie des ensembles*, un axiome permet de former à partir d'une famille d'ensembles ( E_i)_iI un nouvel ensemble qui a pour éléments ceux qui appartiennent à l'un au moins des ensembles  E_i . Ce nouvel ensemble, appelé réunion (des ensembles de) la famille, ( E_i)_iI) est noté ; il est donc défini par :
  

théorie des ensembles*, union

retour à la liste

Deux droites sont sécantes si elles ont un seul point commun. Ce point commun est le point d'intersection des deux droites.
Deux plans de l'espace sont sécants si ils ont une seule droite en commun.

• Deux droites d'un même plan sont soit sécantes soit parallèles.
• Dans l'espace, deux plans sont soit sécants soit parallèles.
  

Par définition, des droites ou des plans sécants sont distincts.

Plus généralement on dit que deux objets géométriques (segment, droite, plan, cercle, etc.) sont sécants s'il sont distincts et admettent au moins un point commun.

intersection, parallèle

retour à la liste

Deux figures géométriques sont semblables si l'une est un agrandissement ou une réduction de l'autre.

Deux figures F et F' sont semblables si on peut trouver une similitude qui envoie F surF' .

retour à la liste

Une similitude est un agrandissement ou une réduction.

Une similitude de rapport k (nombre positif), est une transformation géométrique qui multiplie les longueurs par k ; autrement dit, si des points P et Q quelconques sont transformés en P' et Q', on a :  P'Q' = k PQ.

Dans une espace métrique (E,d), une similitude de rapport k est un transformation géométrique T qui multiplie les distances par k.
autrement dit si P,Q sont deux points quelconques de E ona d(T(P),T(Q)) = k d(P,Q)

retour à la liste

résultat d'une addition ou expression de ce résultat sous forme additive (c'est à dire utilisant une addition, éventuellement plusieurs fois). Il s'agit le plus souvent de nombres, mais on parle aussi de somme d'ensembles, de vecteurs, de fonctions, de polynômes, de matrices, etc.

La somme de deux éléments a et b se note  a+ b. Si l'addition est associative, la somme de plusieurs éléments se note sans mettre de parenthèses

Chaque nombre intervenant dans l'écriture d'une telle somme s'appelle un terme. Si l'addition n'est pas commutative, on fera attention à l'ordre des termes dans l'écriture d'une somme.

Exemples.

25 est la somme de 17 et de 8.
Le nombre 15 se met sous la forme de la somme 1+2+3+4+5.
Si  a et  b sont des nombres (entiers, rationnels, réels ou complexes), l'expression ( a+ b)² représente le même nombre que la somme a²+ b²+ 2ab .

Somme de deux entiers naturels. Si A et B sont des ensembles finis disjoints, A ayant a éléments et B ayant b éléments, la somme a+ b des nombres a et b est, par définition, le nombre d'éléments de la réunion  AB.

retour à la liste

Cette notion concerne les jeux "de type NIM" (le jeu de Marienbad, les Dames, les Échecs, etc.) où deux joueurs s'opposent en modifiant à tour de rôle une situation par un "coup légal", c'est à dire en se conformant aux règles du jeu, jusqu'à ce que l'un des joueur rencontre une situation perdante, c'est à dire où il ne puisse plus jouer.

Si on considère deux jeux de ce type, A et B, on définit le jeu somme , noté A+B, par les règles suivantes :

1. A chaque étape du jeu, la situation courante S du jeu A+B est une paire de deux situations : l'une, S_A, est issue du jeu A, l'autre, S_B, est issue du jeu B.
2. Pour effectuer un coup légal dans A+B, le joueur dont c'est le tour de jouer choisit l'une des situations S_A ou S_B et la modifie par un coup légal : il se conforme aux règles de A s'il a choisi S_A ou aux règles de B s'il a choisi S_B.
3. La situation obtenue dans le jeu choisi forme, avec l'autre situation qui est restée inchangée, la nouvelle situation courante du jeu A+B.
4. Le jeu se poursuit tant qu'il reste une possibilité de jouer, c'est à dire tant que la situation courante n'est pas formé de deux situations perdantes.

retour à la liste

Extrémité d'une arête dans un graphe ou dans un polyèdre.

arête, face, graphes (théorie des), polyèdre

retour à la liste

Syn. partie.

retour à la liste

Opération entre entiers naturels qui à deux nombres entiers aet b, tels que a soit plus grand ou égal à b, fait correspondre leur différence, c'est à dire l'unique entier naturel qui ajouté à b donne a.

Par extension, on appelle soustraction toute opération qui généralise cette soustraction entre nombres entiers naturels.

Lorsque l'addition a de bonnes propriétés (associativité, existence d'un élément neutre et existence d'un opposé pour tout élément : c'est à dire que l'addition est une loi de groupe), la soustraction est une opération inutile car elle revient à l'addition de l'opposé:
la différence a-b de deux éléments a et b est égale à la somme a + (opposé de b).

Exemples : on n'emploie pas le mot soustraction pour des pour des vecteurs, des applications linéaires, des matrices, des polynômes, des fonctions...

retour à la liste

Abréviation pour " si et seulement si " que l'on rencontre souvent dans les écrits de mathématiques. Une phrase qui s'écrit

" A ssi B "

signifie

" si l'énoncé A est vrai, alors l'énoncé B est vrai " et " si l'énoncé B est vrai, alors l'énoncé A est vrai ".

• La démonstration d'un théorème qui s'énonce sous la forme " A ssi B " se fait souvent en deux temps : dans un premier temps, on suppose que l'énoncé A est vrai et on en déduit la véracité de l'énoncé B ; dans le deuxième temps, on suppose que c'est l'énoncé B qui est vrai et on en déduit la véracité de l'énoncé A.

  Ne pas confondre avec le " si " que l'on trouve dans les définitions en mathématiques. Une définition correspond à une phrase du type " A si B " où A désigne un mot du vocabulaire et B est un énoncé qui peut être vrai ou faux ; A consiste simplement en " on appelle tel objet (ou telle situation) de telle façon " ; quand " A si B " est une définition, il n'y a rien à démontrer dans " A ssi B ", puisque la définition sert simplement à condenser l'énoncé B dans un nouveau mot de vocabulaire.

  Ainsi, pour la définition : " Un ensemble est convexe s'il contient tous les segments joignant deux de ses points ", il n'y a rien à démontrer, mais seulement à apprendre ce qu'on appelle " convexe ". Par contre les énoncés " si un ensemble est l'intersection de deux convexes, alors il est convexe " et " une partie de R est convexe ssi c'est un intervalle de R " sont des théorèmes pour lesquels des démonstrations s'imposent ...

retour à la liste

Dans tout ensemble E où l'on dispose d'une loi de composition (c'est à dire d'une opération) notée *, qui admet un élément neutre noté e, on dit que deux éléments a et b de E sont symétriques pour la loi * pour la loi l'un de l'autre s'ils vérifie les égalités suivantes :

a *b = e = b *a .

Dans ce cas, on dira aussi que b est symétrique de a pour la loi *

• En général, un élément peut n'avoir aucun symétrique ou en admettre plusieurs. Toutefois, lorsque l'opération est associative, un élément a qui admet un symétrique b n'en admet qu'un seul, Cet élément est alors appelé le symétrique de a pour la loi *.
  En effet, les relations
       a *b = b *a = e
  et
       a *b' = b' *a = e.
  impliquent, grâce à l'associativité :
       b = b *e = b *(a *b') = (b *a) *b' = e *b' = b'.

  Remarque. Plusieurs opérations pouvent intervenir dans un même ensemble E. Lorsqu'on parle d'élément symétrique, il faut préciser de quelle opération il s'agit.

• Si l'opération considérée se note additivement (c'est à dire comme une addition ), des éléments symétriques pour cette opération sont appelés éléments opposés :
  
  L'élément neutre se note 0 [voir addition].
  a et b sont opposés l'un de l'autre lorsque a+b = b+a = 0.
  
• Si l'opération considérée se note multiplicativement (c'est à dire comme une multiplication ), des éléments symétriques pour cette opération sont appelés éléments inverses :
  
  Si l'élément neutre se note 1 [voir multiplication ].
  a et b sont inverses l'un de l'autre lorsque ab = ba = 1.

retour à la liste

retour à la liste

Enoncé mathématique vrai, c'est-à-dire prouvé. (Le mot théorème vient du verbe grec « théorein », "montrer".)

Un théorème est une phrase qui a une signification mathématique précise et qui est la conclusion d'un raisonnement logique particulier, appelé démonstration. Il est la conséquence logique d'autres propriétés vraies soit parce qu'elles sont prises pour vraies (axiomes et définitions) soit parce qu'elles ont été démontrées auparavant.

retour à la liste

Terme non mathématique. Une théorie est une manière de penser, une méthode, qui permet de se mettre d'accord sur des objets particuliers et sur leurs propriétés. Une "théorie mathématique" sert à créer, décrire, comprendre et organiser des objets mathématiques et permet d'expliquer et d'ordonner leurs propriétés.

Une théorie mathématique ressemble à un immeuble, avec des pièces, des couloirs, des étages, des appartements... Chaque morceau de théorie, objet mathématique ou propriété peut être situé par rapport aux autres morceaux. Certains morceaux servent de point de départ ,de morceaux de base : ce sont les fondations. A partir des fondations on peut bâtir les autres morceaux.
Les propriétés des objets d'une théorie sont les théorèmes. Ce sont soit des propriétés de base, des axiomes, (des propriétés qui sont supposées vraies pour pouvoir démarrer la théorie), soit des conséquences logiques des axiomes.

A l'intérieur d'une théorie très générale, il peut y avoir plusieurs théories particulières, fondées à chaque fois sur des axiomes particuliers.

Les mathématiques elles-mêmes reposent sur des fondations (Logique des propositions, logique des prédicats, théorie des ensembles). Elles permettent aux mathématiciens de se mettre d'accord.

axiome, démonstration, théorème

retour à la liste

La Topologie est une branche des Mathématiques qui fournit un cadre rigoureux aux idées de proximité, de continuité et de discontinuité. Elle construit des "espaces abstraits" dans lesquels des objets, vus comme des ensembles de points, peuvent évoluer et se déformer.

La construction d'un espace topologique utilise essentiellement deux types particuliers d'ensembles de points : les ouverts et les fermés. De manière générale les ouverts (ou les fermés qui sont les ensembles complémentaires des ouverts) sont définis de façon axiomatique (voir ouvert (ensemble -) ) mais peuvent être introduits directement pour chaque espace particulier. Par exemple, les intervalles ouverts de permettent de définir les ouverts de et par là l'espace topologique des nombres réels appelé aussi la droite réelle.

• Extraits d'une interview du mathématicien René Thom par Jacques Nimier

  « - N: C'est quand même vous qui avez introduit le mot de catastrophe ...

     - T: J'ai introduit le mot de catastrophe dans un sens un peu spécial, oui.

     - N: Comment vous est venue l'idée de ce mot ?

     - T: Tout simplement parce que je voulais exprimer l'idée d'une distinction fondamentale, la distinction des topologues entre ouvert et fermé. Un ouvert ça représente, si vous voulez, quelque chose comme un état, un état régulier, une sorte d'équilibre local des dynamiques qui s'y trouvent, tandis que le fermé au contraire, exprime un lieu de points où il se produit quelque chose, une discontinuité. Alors, je suis parti de cette idée que les fermés les plus généraux ne sont pas très intéressants, mais qu'il y a des fermés plus réguliers en quelque sorte qui apparaissent de manière quasi inévitable ... Si on fait des hypothèses sur ce que l'on pourrait appeler la dynamique ambiante, c'est un peu une sorte de généralisation de l'idée de défaut en physique. Dans un milieu ordonné comme un cristal, il y a une structure régulière mais qui s'arrête parfois sur certaines sous-variétés qu'on appelle les défauts; c'est un peu la même idée.

  Alors je voulais exprimer cette idée qu'il y avait des sous ensembles exceptionnels qui étaient associés à des irrégularités de la dynamique et c'est pour cela que j'ai appelé ça des catastrophes; j'aurais pu en effet prendre une terminologie beaucoup plus neutre, ça m'aurait évité bien des ennuis ...»

retour à la liste

Règle qui permet de remplacer chaque point par un autre point.

Le terme de transformation s'emploi dans le plan , dans l'espace, et plus généralement dans tout espace géométrique*.

fonction, application

retour à la liste