Pascal (triangle de -)
Les nombres entiers disposés en quinconce dans ce tableau
|
0
|
|
0
|
|
0
|
|
1
|
|
0
|
|
0
|
|
0
|
|
|
0
|
|
0
|
|
1
|
|
1
|
|
0
|
|
0
|
|
|
0
|
|
0
|
|
1
|
|
2
|
|
1
|
|
0
|
|
0
|
|
|
0
|
|
1
|
|
3
|
|
3
|
|
1
|
|
0
|
|
|
0
|
|
1
|
|
4
|
|
6
|
|
4
|
|
1
|
|
0
|
|
|
1
|
|
5
|
|
10
|
|
10
|
|
5
|
|
1
|
|
satisfont à une loi simple : chaque nombre est la somme
des deux nombres voisins placés au dessus de lui.
En prologenat la première ligne vers la gauche et la droite
avec des "0", cette loi permet de prolonger le tableau vers le bas
aussi loin qu'on le désire.
On obtient ainsi, en effaçant les "0" devenus inutiles, une
infinité de nombres disposés en triangle :
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
2
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
3
|
|
3
|
|
1
|
|
|
|
|
|
|
|
|
|
1
|
|
4
|
|
6
|
|
4
|
|
1
|
|
|
|
|
|
|
|
1
|
|
5
|
|
10
|
|
10
|
|
5
|
|
1
|
|
|
|
|
|
1
|
|
6
|
|
15
|
|
20
|
|
15
|
|
6
|
|
1
|
|
|
|
1
|
|
7
|
|
21
|
|
...
|
|
|
|
|
|
|
|
1
|
|
1
|
|
|
|
.
|
|
.
|
|
.
|
|
|
|
|
|
|
|
C'est ce triangle infini d'entiers naturels qui porte le nom de
triangle de Pascal,
Les nombres qui y figurent, appelés les coefficients binomiaux (car ils
apparaissent comme coefficients dans une formule
célèbre, dite du binôme
de Newton* ), jouent un rôle important dans diverses
branches des mathématiques.
Exemple : Numérotons les lignes successives du
triangle de Pascal, en attribuant à la première ligne
"1" le n° 0, à la ligne suivante "1 1"
le n° 1, et ainsi de suite... La ligne
"1 4 6 4 1" par exemple reçoit
ainsi le n° 4.
Numérotons de la même façon les positions des
nombres dans chaque ligne du triangle : dans la ligne
"1 4 6 4 1", par exemple, le nombre 4
apparaît en position n°1 et aussi en position
n°3.
|

|
THÉORÈME
Soit E un ensemble à n éléments et
soit p un entier naturel, inférieur ou égal
à n.
Le nombre de parties à p éléments de
l'ensemble E est précisément le nombre qui se
trouve en position numéro p dans la ligne
numéro n du triangle de Pascal.
Notation : Ce nombre est noté
et appelé 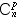 (notation scolaire ;
lire << séènepé >>) (notation scolaire ;
lire << séènepé >>)
Dans le contexte des probabilités (part exemple
lorsqu'on tire au hasard p boules dans une urne contenant n
boules équiprobables), une partie à p
éléments de E s'appelle aussi une combinaison
de p
éléments
pris parmi les n
éléments
de E et le nombre
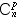 s'appelle le nombre de
combinaisons de p éléments parmi n
(ou, improprement, "de n éléments pris p
à p" . s'appelle le nombre de
combinaisons de p éléments parmi n
(ou, improprement, "de n éléments pris p
à p" .
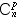 est aussi noté sous la forme est aussi noté sous la forme 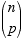 (notation professionnelle : lire << coefficient binomial n
p >> ou, en abrégé, << binomial n p >>). (notation professionnelle : lire << coefficient binomial n
p >> ou, en abrégé, << binomial n p >>).
|
- Les coefficients binomiaux sont connus depuis la haute
Antiquité, et la découverte de la loi de formation
du triangle de Pascal est en fait bien antérieure au
XVIIème siècle, C'est pourtant le nom de
Pascal (philosophe théologue, physicien et
mathématicien, 1623-1662) qui resta attaché à
ce triangle de nombre, eu égard aux travaux qu'il y
consacra. L'étude des coefficients binomiaux,
après les contributions de Newton (physicien, astronome
et mathématicien anglais, 1642-1727) se poursuit encore de
nos jours. (voir par exemple les sujets de recherche
étudiés par un atelier MATh.en.JEANS de
Neuchâtel
en Bray en 2001-2002.
retour au glossaire
![]()
(notation scolaire ; lire << séènepé >>)
s'appelle le nombre de combinaisons de p éléments parmi n (ou, improprement, "de n éléments pris p à p" .
est aussi noté sous la forme
(notation professionnelle : lire << coefficient binomial n p >> ou, en abrégé, << binomial n p >>).