1er cas : le nombre de côtés n est pair
Exemple pour n = 8 :
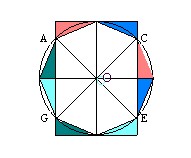
Dessin 9
3. Passage d'un polygone régulier à un rectangle non donné à l'avance
|
1er cas : le nombre de côtés n est pair Exemple pour n = 8 :
|
Dessin 9 |
|
2ème cas : le nombre de côtés n est impair Exemple n = 5 Les méthodes utilisées auparavant se sont révélées difficiles pour un nombre impair de côtés (pour n>3). On a donc essayé de trouver une méthode généralisable au plus grand nombre de polygones. [Nous l'expliquons ici pour n=5]. Soit ABCDE un pentagone régulier donc inscriptible dans un cercle de centre O et de rayon R. En joignant le centre aux différents sommets, on obtient cinq triangles isocèles tous isométriques que l’on sait transformer séparément en rectangle. Si on choisit comme base du triangle le côté mesurant R on obtient cinq rectangles de même dimension qui, "empilés" donnent un rectangle de même aire que le pentagone. |
Dessin 10 |