[La méthode qui suit n'est, en fait, pas applicable à tout hexagone]

Soit ABCDEF un hexagone quelconque. Par trois points, il passe un cercle et un seul. Choisissons le cercle passant par ACE, de centre O et de rayon R. Les segments [OA], [OB], [OC], [OD], [OE] et [OF] déterminent 6 triangles ayant un côté de longueur commune R. On sait transformer chacun de ces triangles en rectangle en choisissant comme longueur, le côté de mesure R et en "empilant" ces rectangles on obtient un rectangle de même aire que l’hexagone.

Cette méthode devient inefficace si n>6

[Pour que la méthode marche pour l'hexagone, il faut que les points A,C et E ne soient pas alignés et que chacun des segments [OA], [OB], [OC], [OD], [OE] et [OF] soit contenu dans l'hexagone.

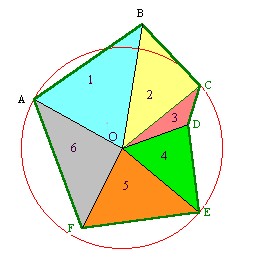
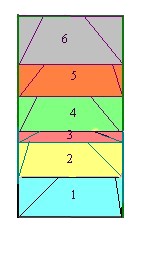
Dessin 11