- Considérons un triangle rectangle ABC et un triangle DBC de même hauteur et de même base. On observe une partie commune au deux triangles : COB.
- Par symétrie centrale, on construit le triangle D’C’O symétrique de DCO par rapport au point O. On observe encore une partie commune OBEC’.
- Recommençons l’opération par la symétrie de centre E. On obtient ED’’B’ qui est le symétrique du triangle EBD’, ils ont une partie commune C’FB’E.
On pourrait recommencer l'opération. FC’’D’’’ serait le symétrique de D’’FC’ par rapport au point F. Il y aurait encore une partie commune : FC’’KB’.
Il nous resterait 2 triangles quelconques ; pour que cette méthode réussisse il faudrait que ces 2 triangles soient superposables. Or on ne sait pas transformer un triangle quelconque en un autre triangle de même aire. On peut penser qu’en continuant cette méthode indéfiniment, à la limite, il ne restera plus rien à recouvrir. On aurait réussi à transformer un triangle en un autre mais notre découpage comporterait un nombre infini de morceaux or le problème posé est : découpage en un nombre fini de parties.(dessins 7 et 8)
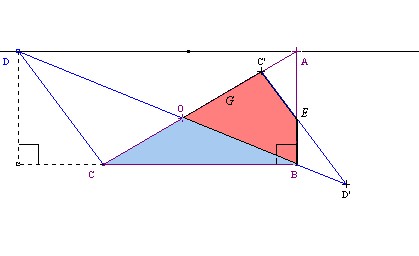
Dessin 7
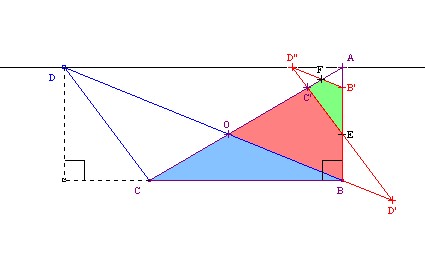
Dessin 8