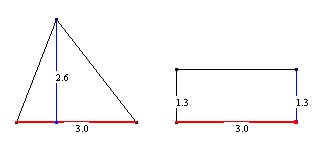
On se donne un triangle et un rectangle de même aire [et de même base].

Dessin 1
|
On a cherché le plus grand carré qui soit contenu à la fois dans le triangle et dans le rectangle (voir dessin 2). Il reste des parties vides à remplir, alors on continue le remplissage avec des petits carrés (dessin3). Peut-on superposer les parties restantes ? On voit tout de suite qu'il est difficile de découper les morceaux restants ; on ne peut plus y loger des carrés de même dimension.
A la fin on constate que certaines parties du triangle se retrouvent dans le rectangle qui est donc recouvert partiellement. (dessin 4). Que faire avec des petits bouts restants, même très petits ? Peut-être pourrait-on aller plus loin mais on n’est pas sûr de recouvrir le rectangle en un nombre fini d’opérations. Cette approche n’est pas concluante puisque l’on cherche un découpage en un nombre fini de parties. |
Dessin 2
Dessin 3
Dessin 4 |
Passage d’un triangle ABC à un rectangle quelconque :
|
1er cas. Le triangle ABC a tous ses angles aigus. Soit I et J les milieux respectifs de [AB] et [AC]. (AH) la hauteur issue de A coupe (IJ) en K. La droite (IJ) coupe respectivement en Fet E les droites perpendiculaires à (BC) passant par B et C. [On peut montrer que] la symétrie de centre I transforme le triangle AIK en BFI et la symétrie de centre J transforme AKJ en CEJ. [Le découpage est ainsi justifié, voir dessin 5.]
2ème cas. Le triangle ABC a un angle obtus en B. Comme précédemment la droite (IJ) est la droite des milieux du triangle ABC. (CK) est parallèle à (AB).Le triangle CEK se déduit du triangle BFI par la translation de vecteur BC. [Le découpage est ainsi justifié, voir dessin 6.] [NDLR : Et si le triangle était obtus en A, que faire ?] |
|