Nous avons cherché à résoudre des équations irrésolvables par le calcul. C'est pourquoi nous avons décidé d'utiliser un autre outil mathématique : la méthode graphique.

Pour illustrer notre démonstration nous avons choisi l'exemple de l'équation :   cos(x)=x.
C'est à dire trouver le zéro de la courbe représentative de f(x)=cos(x)-x.

On peut prouver qu'il n'existe qu'un seul zéro (démonstration).

Nous sommes partis en premier lieu avec une méthode de référence: la dichotomie. Elle consiste à prendre un intervalle [a;b] tel que le zéro appartienne à [a;b] puis à couper l'intervalle en deux :

1ère étape :

             

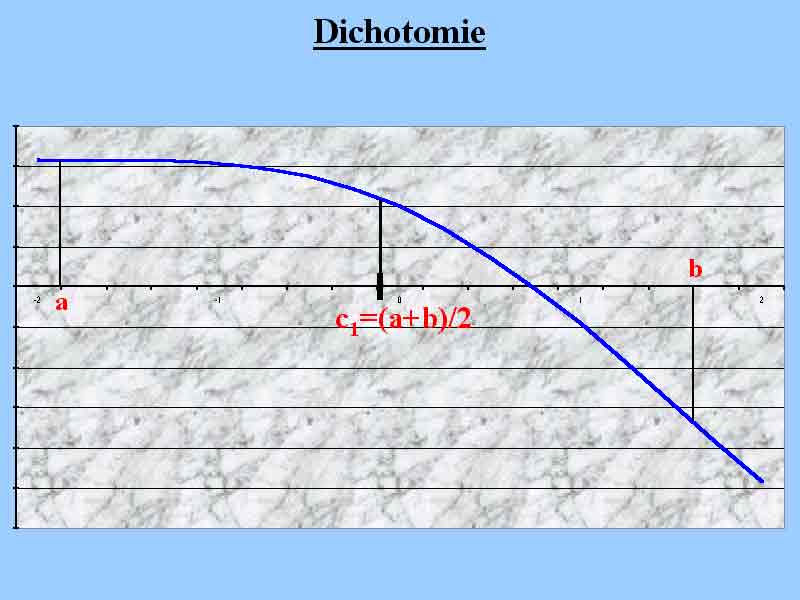
On choisi alors l'un des deux intervalles (celui qui contient le zéro) pour itérer la procédure :

2ème étape :

Cette méthode converge ... (La preuve)

      Pour aller plus vite, nous avons constaté qu'il fallait s'approcher plus rapidement du zéro... donc dans notre exemple se rapprocher de plus en plus de la borne de droite de l'intervalle [a;b]. Nous nous sommes donc dit qu'il fallait choisir à chaque étape l'une des deux bornes et s'en approcher. Et logiquement nous avons donc décidé de nous rapprocher plus du point dont l'ordonnée est [en valeur absolue] la plus petite. Par analogie, nous avons eu l'idée de barycentre.

     page suivante :Méthode astucieuse par le barycentre