|
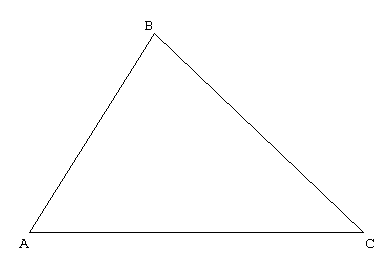
Nous nous somme concentrés sur un triangle quelconque dons les mesures sont : - pour les côtés
- pour les angles
|
 |
I -Le problème posé :
Notre problème est de plier une figure plane en trouvant le meilleur résultat possible.
|
Nous nous somme concentrés sur un triangle quelconque dons les mesures sont : - pour les côtés
- pour les angles
|
 |
Pour évaluer la qualité d'un pli, nous avons défini son rendement.
Définition. Le
rendement d'un pli, c'est le quotient: ![]()
A propos de ce rendement, nous avons démontré un
théorème
Théorème : Le rendement doit obligatoirement être compris entre 0.5 et 1.
Démonstration
première partie: le quotient ![]() est
inférieur à 1.
est
inférieur à 1.
En effet, l'aire pliée est plus petite que l'aire totale.
Donc ![]() est inférieur à
est inférieur à ![]()
C'est à dire que le rendement est inférieur à 1
Deuxième partie: le rendement est supérieur à 0,5.
En effet, on ne peut pas cacher plus de la moitié de l'aire totale.
Donc![]() est supérieur à
est supérieur à ![]() de l'aire totale
de l'aire totale
Or ![]()
Donc l'aire pliée est supérieure à ![]() de l'aire totale
de l'aire totale
et ![]() est supérieur à
est supérieur à ![]() ou le rendement est supérieur à
ou le rendement est supérieur à
![]() .
.