Comptes Rendus MATh.en.JEANS 05-01

 Le triangle de Reuleaux

tourne pas rond

Enseignants : Hubert Proal.

Chercheur [correspondant] P. Verovicz (Université de Savoie)

Atelier MATh.en.JEANS  année scolaire 2004-2005.

[Article vérifié et annoté : les passages entre crochets sont des éditeurs]
[ L'icône renvoie au Glossaire MATh.en.JEANS , à un document ]

1. Le triangle de Reuleaux
2. La construction du triangle de Reuleaux
3. Périmètre du triangle de Reuleaux
4. Aire du triangle de Reuleaux
5. Quelques propriétés du triangle de Reuleaux
6. Peut-on fabriquer d'autres polygones de Reuleaux?
7. Conjecture
8. [ D'autres études sur le sujet ]

- On fait un triangle équilatéral ABC

- On pointe A avec un compas et on trace l'arc de cercle BC

- Puis ainsi de suite pour les autres points B et C

- Quand tout ceci est terminé nous pouvons distinguer un magnifique triangle de Reuleaux.

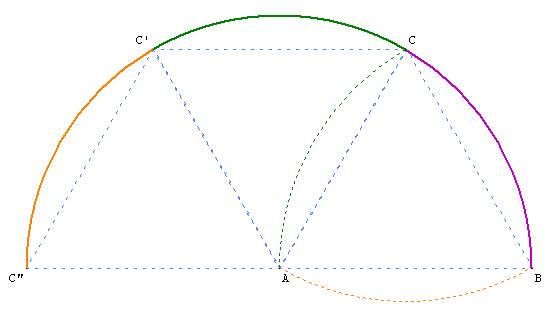
Le périmètre du triangle de Reuleaux correspond au périmètre d'un demi cercle. Soit a×p  où a est la longueur AB.

[Comme le montre le dessin où les arcs de cercle de même couleur ont la même longueur.]

De la même manière, [en utilisant le même procédé de correspondance de zones de même couleur] on peut constater que l'aire d'un triangle de Reuleaux est identique à [l'aire du demi cercle de rayon a] moins [l'aire] du parallélogramme jaune

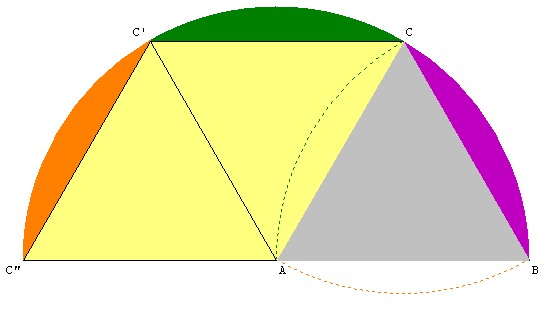
[Pour calculer l'aire du parallélogramme jaune, il faut connaître la hauteur du triangle gris]

Calcul de la hauteur Pour calculer la hauteur h nous utilisons le théorème de Pythagore dans le triangle rectangle AHC

Ainsi l'aire du triangle de Reuleaux est :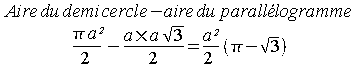

Il est à « diamètre » constant. En particulier il peut tourner entre deux droites parallèles.

Le triangle de Reuleaux peut aussi tourner dans un carré et l'enveloppe que l'on obtient est le carré.

Si on part d'un hexagone ou d'un carré, on constate que le diamètre n'est pas constant.

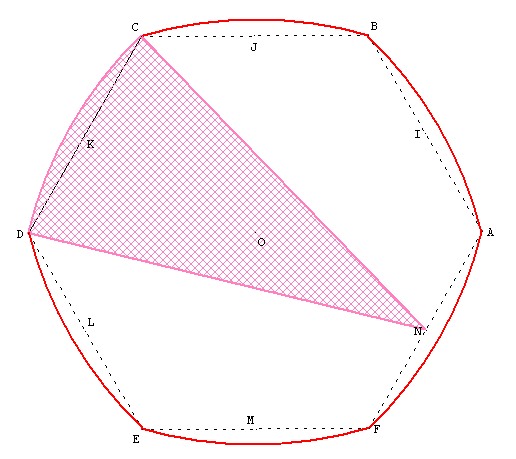
On peut généraliser à tous les polygones réguliers avec un nombre pair de côté. 

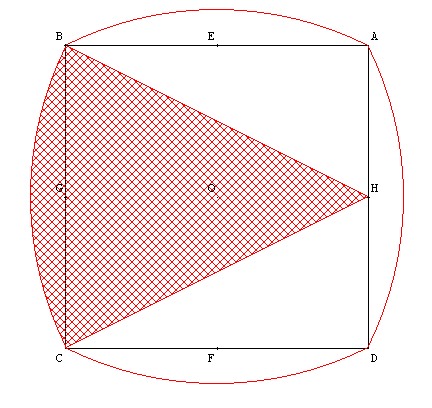
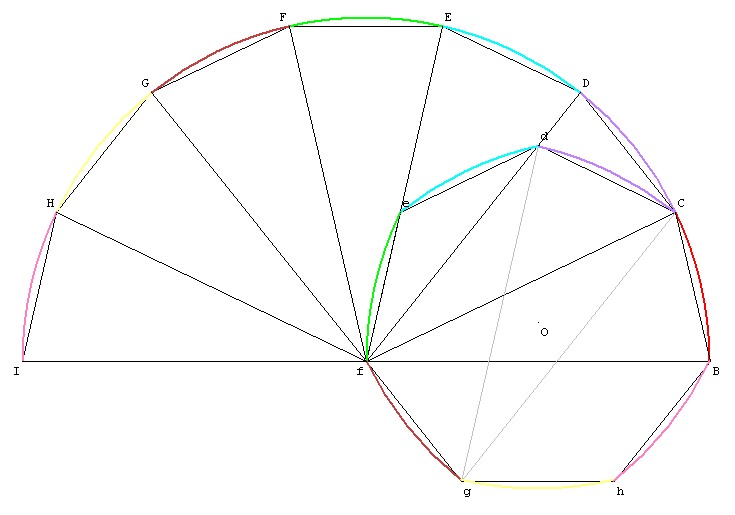
Par contre, pour les polygones avec un nombre impair de côté, le diamètre est constant.

Par exemple, l'heptagone de Reuleaux a un diamètre constant CG.

Comme pour le triangle de Reuleaux, on peut montrer que le périmètre est  fois le diamètre :

Les périmètres des figures qui sont à diamètre constant sont  fois le diamètre.

Remarque : Par contre, comment sont les aires des figures à diamètre constant ?

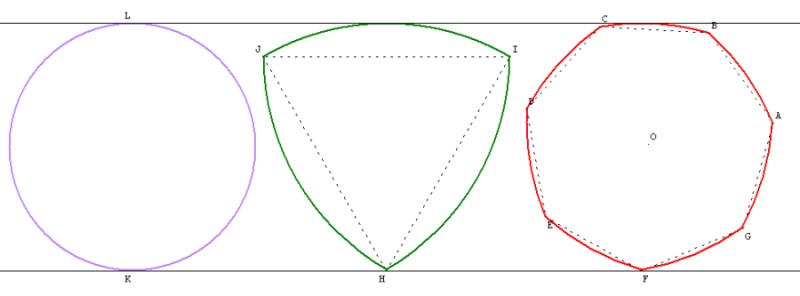
On a démontré que l'aire du triangle de Reuleaux était plus petite que celle du cercle (de même diamètre), ce qui veut dire qu'il est plus « rentable » de construire des boutons de la forme du triangle de Reuleaux.

- Et bien d'autres, il suffit de demander "Reuleaux" à un moteur de recherche

trangle reuleaux diamètre largeur perimètre aire