Comptes Rendus MATh.en.JEANS 98-09

Enseignants : Jean-Pierre BOURBOUZE (clg. Robespierre), Adrien FRYC (Clg. Elsa Triolet) ; Alain HUET (Lyc. Paul Eluard), Christophe MALLET, (clg. Robespierre)
Chercheur : François PARREAU (Inst. Galilée, Univ. Paris 13, 93-Villetaneuse).
Jumelage MATh.en.JEANS entre les collèges Robespierre d'Epinay sur Seine (93), et Elsa Triolet de St-Denis (93) et le Lycée Paul Eluard de St-Denis (93). Ateliers de Pratique Scientifique, année scolaire 1997-1998.

---

[Article reçu le 15 avril 1998, publié vérifié et annoté le 17 septembre 2004 : les passages entre crochets sont des éditeurs]

[ L'icone renvoie au Glossaire MATh.en.JEANS , à un document ]

---

[Comme dans le classique jeu de solitaire, il s'agit de déplacer des pions suivant certaines règles pour aboutir à une position voulue. Le matériel du solitarium est rudimentaire :

- des cases disposées en cercle (comme les secteurs d'une roue de loterie).
- des pions.

Au début du jeu, on répartis des pions, au hasard, dans les cases. Ensuite, à chaque tour de jeu, on déplace 2 pions de son choix en respectant les règles suivantes.

(1) Chaque pion est déplacé vers une case voisine.
(2) Les 2 pions sont déplacés en sens contraire.

Le but du jeu est d'amener tous les pions dans une même case.

• Dans la version simple du jeu, la position de départ comporte exactement 1 pion par case.
  Peut-on toujours gagner ? Comment ?
• Dans la version générale, le nombre pions est quelconque et leur disposition de départ est quelconque. On peut aussi corser la difficulté en s'imposant à l'avance une case finale ... ]

[Nous avons étudié la version simple du solitarium: il y a au départ 1 pion dans chaque case. Nous avons trouvé une méthode pour gagner lorsque le nombre de case est impair., Il semble impossible de gagner lorsque le nombre case est pair.].

On a "n" pions répartis sur "n" cases.

1. Méthode par symétrie [(N impair)].

Hypothèses.

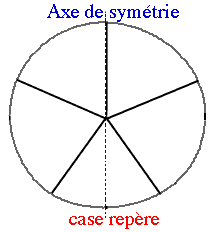
On choisit une case d'arrivée. On suppose toutes les cases d'égale dimension et on se donne comme axe de symétrie du cercle le diamètre, bissectrice de la case d'arrivée. En dehors de cette case, on a donc divisé ainsi le cercle en deux parties comprenant le même nombre de cases.

Description de la méthode par symétrie avec l'exemple N=5.
1er	coup 2ème	coup 3ème	coup

[La] détermination du nombre de coups nécessaire pour gagner [se fait de la manière suivante.]

[Théorème 1]. Supposons que le nombre de cases, n, soit impair. Le nombre de coups C [utilisé par la méthode par symétrie pour le solitarium simple] est :

Exemple. Pour n=5, le nombre de coups utilisé vaut C = (N²-1)/8, soit C = (25-1)/8.= 3, [ce qui est conforme aux figures ci-dessus]

Démonstration.

On constate que lorsqu'un pion est situé dans une case quelconque à k cases de la case d'arrivée, il faut k coups pour l'y amener. Donc, si k=1, il faut un coup. Si k=2, il faut deux coups ... etc. [note 2]

[On se donne une situation de départ àù il y a une case d'arrivée et p autres cases numérotées de 1 à n, avec 1 pion dans chacune de ces cases,] On peut calculer le nombre de coups pour gagner, donc pour amener tous les pions de toutes les cases dans la case d'arrivée en additionnant 1+2+3+4+...+n jusqu'à la case numéro n.

Or [il est connu que] cette somme, somme des n premiers entiers vaut :

1+2+3+4+...+n = n(n+1)/2

[Plaçons-nous maintenant dans la situation du solitarium simple.] Si n est le nombre de cases, il y a donc (N-1) pions à déplacer [en tout,] donc (N-1)/2 de chaque coté. Et le rang de celle [la case] qui est la plus éloignée de la case d'arrivée est donc (N-1)/2. C'est donc ce nombre qui va remplacer n dans la formule ci-dessus.

Après calcul on trouve pour C la valeur C = (N²-1)/8.
Pour que la démonstration soit totale, il reste à démontrer cette généralisation par récurrence. (note 3)

[Théorème 2]. Supposons que le nombre de cases, N, soit impair. Le nombre de coups K nécessaires pour gagner [au solitarium simple] est :

C = (N²-1)/8  . [note 4]

2. Le cas n pair

[Conjecture 3]. Pour N pair, il est impossible de gagner.

[Théorème 4]. Pour N =4, il est impossible de gagner.

Démonstration.

[On va construire toutes les positions possibles du jeu. ]

Il n'existe que 3 types de coups, montrés sur la figure ci-contre [note 5].
En partant de la situation initiale, ces types de coups conduisent à l'une des 3 solutions suivantes [note 6].	(1)	(2)	(3)

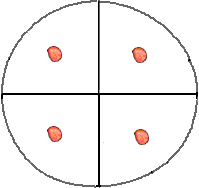
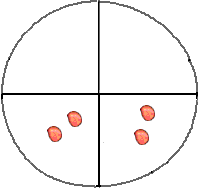
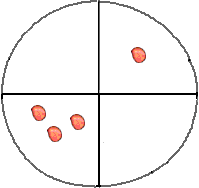
[Il est maintenant facile de vérifier qu'aucune disposition nouvelle n'apparait lorsqu'on effectue un nouveau coup à partir des situations précédentes. [note 7]. Aucune des solutions trouvées n'est gagnante, il est donc impossible de gagner. ]

Note 1. Cet article est tiré des transparents présentés par les élèves lors de leur exposé au congrès MATh.en.JEANS 1998.

retour à l'appel de cette note

Note 2. Les auteurs utilisaient la même lettre n pour numéroter les cases et pour désigner le nombre de cases dans chacune des situations examinées. Nous avons préféré utiliser des lettres différentes suivant les parties du raisonnement.

retour à l'appel de cette note

Note 3. Ce qui est, classiquement, démontré par récurrence sur n c'est la formule 1+2+3+4+...+n = n(n+1)/2. Mais, une fois cette formule établie, il n'est nullement besoin de faire appel à une autre récurrence pour avoir le nombre de coups.

retour à l'appel de cette note

Note 4. Ce résultat donne le nombre de coup utilisés par la méthode de symétrie mais affirme aussi que cette méthode permet de gagner en un nombre minimum de coups. Les auteurs ne fournissent pas de démonstration explicite de cette affirmation. En voici une.
Supposons que, par une certaine méthode M, nous ayons réussi à amener tous les pions dans une certaine case, que nous appelons case d'arrivée. Donnons à cette case le numéro 0 et numérotons de proche en proche les cases du jeu dans l'ordre les aiguilles d'une montre. Dans la situation de départ, il y a 1 pion dans chacune des cases numérotées 1,2,..., (N-1)/2. Comme au début de la preuve du théorème 1, nous pouvons affirmer que pour amener le pion de la case numéro k dans la case d'arrivée, la méthode M utilise au moins k coups (on utilise pour cela le fait que k est inférieur à N-k, ce qui fait que, parmi tous les voyages imaginables du pion de la case numéro k vers la case numéro 0, c'est finalement celui qui utilise successivement les cases numérotées  k-1,  k-2,..., 2,1, 0 qui est le plus court).
Les pions des cases 1,2,..., (N-1)/2 étant tous distincts, le nombre total de coups utilisés par la méthode M pour les amener tous dans la case d'arrivée est donc au moins égal à la somme 1+2+...+(N-1)/2, soit, d'après le théorème 1, (N²-1)/8.

retour à l'appel de cette note

Note 5. Un coup est déterminé par les deux cases d'origine des déplacements de pions et par le sens de ces déplacements. Deux coups qui ont le même écartement des cases d'origine et mêmes sens de déplacements sont considérés comme de même type. Depuis la position de départ du jeu, seuls 3 types de coups sont possibles. Mais au cours du jeu un quatrième type de coup doit être pris en compte, comme indiqué ci-contre. Un coup de type (4) peut être vu comme "l'inverse" d'un coup de type (3) (alors que chacun des types (1) ou (2) est son propre "inverse").

retour à l'appel de cette note

Note 6. Deux dispositions de pions qui se correspondent pas symétrie ou par rotation sont considérées comme une seule "solution".

retour à l'appel de cette note

Note 7. Par exemple, à partir d'une disposition de pions de type (B), seuls des coups de type ((1), (2) ou ((4) (voir note 5) sont applicables. Ils conduisent respectivement à des positions de type (B), (A) ou (C).

retour à l'appel de cette note

jeu combinatoire solitaire pion cases cycle nombres triangulaires invariant arrangements avec répétition