Stratégie de Nicomède
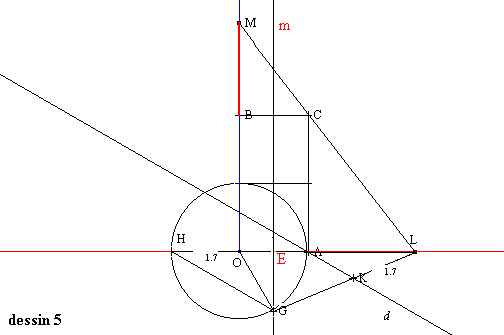
Pour la solution de Nicomède (Vième siècle avant J-C) (dessin 5), on commence par construire un rectangle OACB tel que OA = a et OB = 2a, puis on trace le cercle C de rayon [OA] et de centre O. La médiatrice m de [OA]coupe ce cercle en deux points, dont G, point situé dans le demi plan de frontière (OA) qui ne retient pas B en otage.La droite m coupe (OA) en E.
On récidive en traçant [AH] qui est un diamètre de C , puis en traçant la droite d parallèleà (HG) passant par A.

L est alors un point stratégique, placé sur (OA) tel que le segment [GL] coupe la droite d en K, mais de manière à ce que KL = OA = a. L’assaut final est donné en construisant (LC) qui coupe (OB) en M, car comme je vais vous le montrer,
MB = a![]() . Soit
a = 1. GEL est un triangle rectangle en E, donc GL² = GE² + EL². Or GE est la
hauteur d’un triangle équilatéral de côté 1, donc GE =
. Soit
a = 1. GEL est un triangle rectangle en E, donc GL² = GE² + EL². Or GE est la
hauteur d’un triangle équilatéral de côté 1, donc GE = ![]()
EL = AL +![]()
GL² = ![]() +( AL
+
+( AL
+![]() )² =
)² = ![]()
GL² = AL² + AL + 1
D’après le théorème de l’agent Thalès:![]() car
(GH) est parallèleà (AK). Or: LK = a =1.
car
(GH) est parallèleà (AK). Or: LK = a =1.
HL = HA + AL = 2a + AL = 2 + AL. Nous avons:![]()
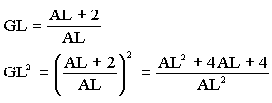
Nous avons donc deux valeurs de GL²: AL² + AL + 1 = ![]() d'où
d'où
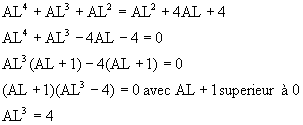
AL = ![]() (a = 1)
(a = 1)
Or les deux triangles rectangles MBC et CAL sont semblables car (MB) et (AC) d’une part, (BC) et (AL) d’autre part, sont parallèles, et les droites (MC) et (CL) sont confondues
On obtient grâce au théorème de Thalès: ![]() puis
puis ![]() puis x
=
puis x
=![]() d'où x3
=
d'où x3
=![]() = 2 et x
=
= 2 et x
= ![]()
Malheureusement, on ne peut pas obtenir le point L à la règle et au compas sans tâtonner. Mais une mission de reconnaissance nous a montré que si on place L quelle que soit la place de K sur d, L décrit un courbe appelée conchoïde de Nicomède. (dessins 6 et 7 ).Le point L cherché est l’intersection de cette conchoïde et de (OA).Cependant, la règle et le compas ne permettent pas de construire l’infinité de points que constitue cette droite. Par contre, l’agent Nicomède nous a laissé un gadget très utile pour résoudre cette mission (et éventuellement d’autres):le traceur de Nicomède.
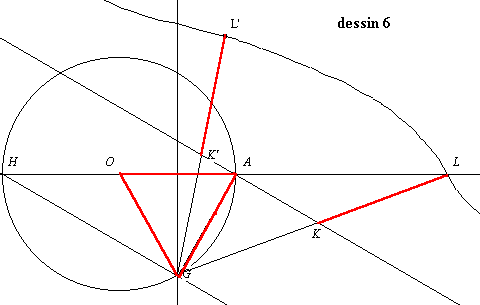
(Construction "à main levée " de la conchoïde de Nicomède)
Voici maintenant la conchoïde de Nicomède tracée dans un repère :
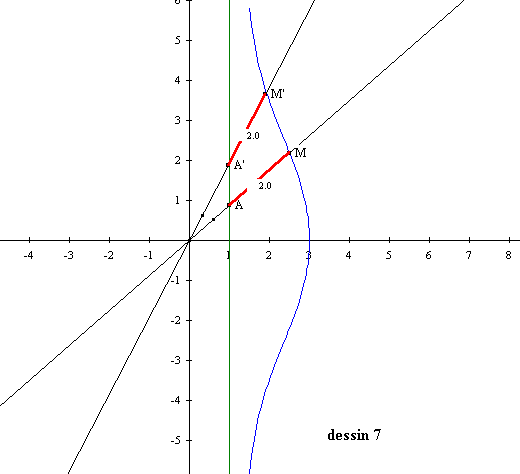
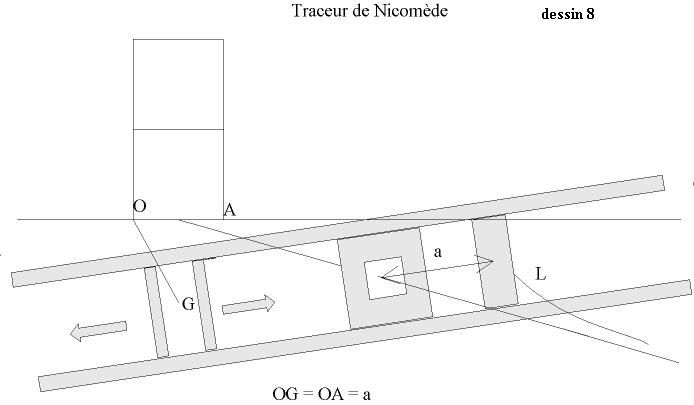
Le traceur de Nicomède est constitué de deux pointes et d’une mine de crayon. L’une des pointes est mobile et constitue avec la deuxième pointe la distance GK. L’autre est fixe et constitue avec la mine la distance fixe KL = a. La mine est mobile en fonction de a. On pose les deux pointes sur G et la droite d, puis on trace la conchoïde donnant le point L. (dessin 8)
La mission proposée semble donc impossible avec une règle et un compas. Elle peut cependant être obtenue manuellement grâce au traceur de Nicomède, superbe gadget beaucoup plus discret qu’un ordinateur.
Note du chercheur:
Sans le démontrer explicitement, on peut penser que la construction à la
règle et au compas de![]() est impossible.
est impossible.
En effet,![]() appelée
constante de Delian est un nombre non euclidien (*).
appelée
constante de Delian est un nombre non euclidien (*).
La classification des nombres est très importante en mathématiques, elle permet de résoudre et d'analyser les solutions de nombreux problèmes complexes ( par exemple l'analyse des solutions des équations algébriques).
(*) Les nombres euclidiens peuvent être obtenus par résolutions successives d'équations du second degré ou par construction géométrique.