Comptes Rendus MATh.en.JEANS 04-05

Enseignants : Dominique GUY et Mickaël PRADO (Lycée Romain Rolland, Argenteuil)

Chercheur : Loïc ALLYS (Université de Maine, Le Mans).

Atelier MATh.en.JEANS de pratique scientifique, année scolaire 2003-2004.

---

[Article vérifié et annoté : les passages entre crochets sont des éditeurs]

[ L'icone renvoie au Glossaire MATh.en.JEANS , à un document ]

---

Plan

 Sujet
1- cas des parallélogrammes particuliers.
      - définition
      - calcul de l'aire
2- les cas généraux
      - comment les reconnaître ?
      - calcul de l'aire.

Comment trouver l'aire d'un quadrilatère quand on ne dispose que d'une règle graduée ? [note 1]

Problématique: peut-on toujours utiliser les formules connues pour calculer les aires ? (Problème : Ici on ne connaît pas la hauteur [des figures] et on ne dispose ni d'équerre ni de compas)

1. Cas des parallélogrammes particuliers

1A. Le carré

Propriété caractéristique utilisée :

Un carré est un rectangle particulier dont deux côtés consécutifs ont la même longueur.

Comment les reconnaître ? Il suffit de mesurer avec la règle graduée les diagonales et les cotés pour vérifier cette propriété. [note 2] Après avoir vérifié qu'il s'agit bien d'un carré, il suffit d'utiliser la formule magique : A = a2 [a est la longueur du côté]

Schéma d'un carré :

1B. Le rectangle

Propriété [caractéristique] des rectangles :

Un rectangle est un quadrilatère particulier dont les diagonales ont même longueur et se coupent en leur milieu et dont les cotés opposé ont la même longueur.

Comment les reconnaître ? Il suffit de mesurer avec la règle graduée les cotés et les diagonales. [note 3] Après avoir vérifié qu'il s'agit bien d'un rectangle, il suffit d'utiliser la formule magique : A = Lxl. [L et l désignent la longueur et la largeur]

Schéma d'un rectangle :

1C. Le losange

Propriété [caractéristique] du losange :

Un losange est un quadrilatère qui possède quatre cotés égaux, et deux diagonales qui se coupent en leur milieu.

Comment les reconnaître ? Il suffit de mesurer avec la règle graduée les cotés et les diagonales. [note4] Après avoir vérifié qu'il s'agit bien d'un losange, il suffit d'utiliser la formule magique : A = Dxd [D et d désignent les longueurs des diagonales]

Schéma d'un losange

2. Les cas généraux.

2A. Le trapèze rectangle

Propriété caractéristique utilisée :

Un trapèze est un quadrilatère qui possède deux angles droits et deux cotés parallèles.

Comment les reconnaître ? Il suffit de démontrer que nous avons deux angles droits avec la réciproque de Pythagore : dans le triangle abc (rectangle en b) ab2+ bc2 doit être égal à ac2 . Après avoir démontrer qu'il s'agit bien d'un trapèze rectangle, on applique la formule magique : A = (Base+ petite base) x h [h est la hauteur, ici égale à ab]

[Schéma d'un trapèze rectangle :]

2B. Quadrilatères généraux

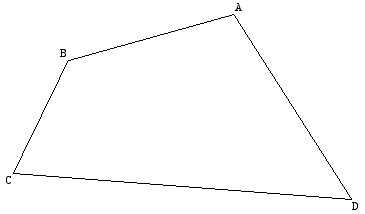
Nous allons diviser le quadrilatère en deux triangles et travailler sur un seul des deux. [L'aire du quadrilatère s'obtiendra en ajoutant les aires des deux triangles]

Supposons que l'on sache où se situe la hauteur h [soit h=BH] du triangle [ABC]. On peut ainsi la mesurer. Avec la formule de pythagore on a [... note 5] (les cotés du triangle sont notés a, b, c et on pose AH=c' et CH=b') (1) On en déduit (en effet, on a (2) ) Posons ; avec ce qui précède, on obtient : (3)   En ajoutant (1) et (2) on obtient :] , d'où    (4) En retranchant (2) de (1) on obtient : , d'où    (5)

Les formules (3), (4) et (5) permettent de calculer n, puis c' et b' à partir de a, b et c. La formule (1) permet alors de calculer h, puis l'aire du triangle ABC, égale à . Tous calculs faits, on obtient : ]

[2C. Polygones quelconques (note 6)]

Note 1. Ce sujet de recherche est inspiré du sujet n°32 du projet Espace : dans les communautés primitives mayas, la surface d'un champ bordé par 4 côtés s'obtenait avec des règles extrêmement simples : faire la moyenne de deux côtés opposés puis des deux autres côtés, puis multiplier les nombres obtenus. La surface de champs de formes plus complexe s'obtenait par division en régions à 4 côtés.
La recherche des auteurs a en fait concerné les polygones quelconques, le cas des quadrilatèresétant considéré comme crucial. Les quadrilatères dont il est question ici sont supposés non croisés.

retour à l'appel de cette note

Note 2. Les auteurs se ramènent ici à la caractérisation des rectangles dont ils parlent plus loin (§1B): égalité des diagonales et intersection des diagonales en leur milieu. La vérification de la forme "carré" nécessite ainsi le tracé des diagonales et 8 mesures de segments. Il serait sans doute suffisant de vérifier l'égalité des cotés (4 mesures) et celles des diagonales (2 mesures). cf. carré

retour à l'appel de cette note

Note 3. La vérification de la forme "rectangle" nécessite ainsi le tracé des diagonales et 8 mesures de segments. Peut-être serait-il suffisant de vérifier l'égalité des cotés opposés (4 mesures) et celles des diagonales (2 mesures). cf. rectangle

retour à l'appel de cette note

Note 4. La vérification de la forme "losange" nécessite ainsi le tracé des diagonales et 8 mesures de segments. Peut-être serait-il suffisant de vérifier l'égalité des cotés (4 mesures). cf. losange

retour à l'appel de cette note

Note 5. Nous avons agrémenté les calculs des auteurs de quelques explications et ajouté figure et formule finale.

retour à l'appel de cette note

Note 6. Comme les auteurs l'avaient remarqué au début de leur recherche, pour obtenir l'aire un polygone quelconque, la connaissance de certaines diagonales est utile : avec des diagonales bien choisies, le découpage d'un polygone quelconque (convexe ou non) en triangles apparaît en effet toujours possible. L'aire totale s'obtient alors en faisant la somme des aires triangulaires, calculées chacune avec la méthode proposée ci-dessus (§2B).

retour à l'appel de cette note

AIRE DISTANCE POLYGONE QUADRILATÈRE TRIANGULATION TRIANGLE THEOREME DE PYTHAGORE