Tous les chemins mènent à Rome, mais combien y en a-t-il ?  ,  Comptes Rendus MATh.en.JEANS 02-03

1 Le réseau carré

Présentation Le réseau carré est un quadrillage dont la longueur et la largeur [des cases] ont les mêmes mesures.

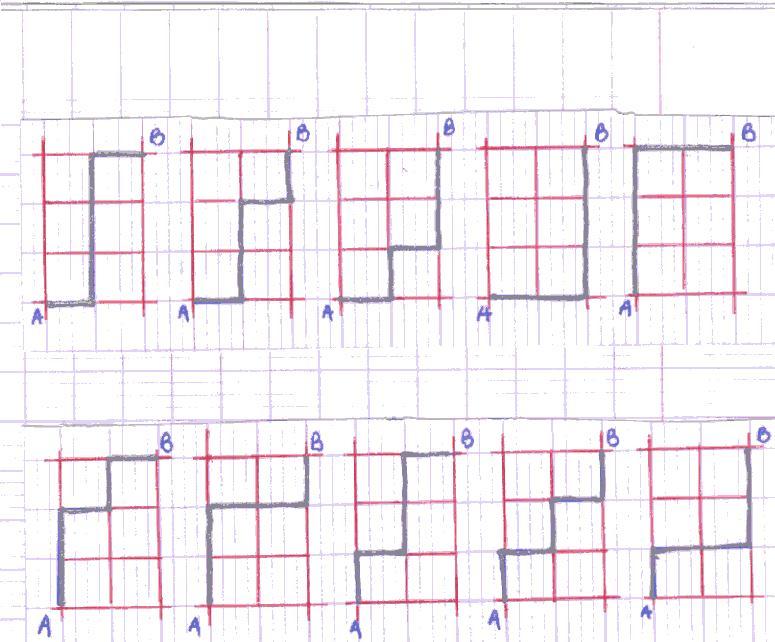
Définition. On considère qu'un marcheur ivre [cf. note 1] ne peut se déplacer que vers la droite et vers le haut.

Donc, le [problème du] réseau carré consiste à trouver tous les chemins possibles pour aller d'un point A à un point B (voir les exemples de figures ci-dessous)

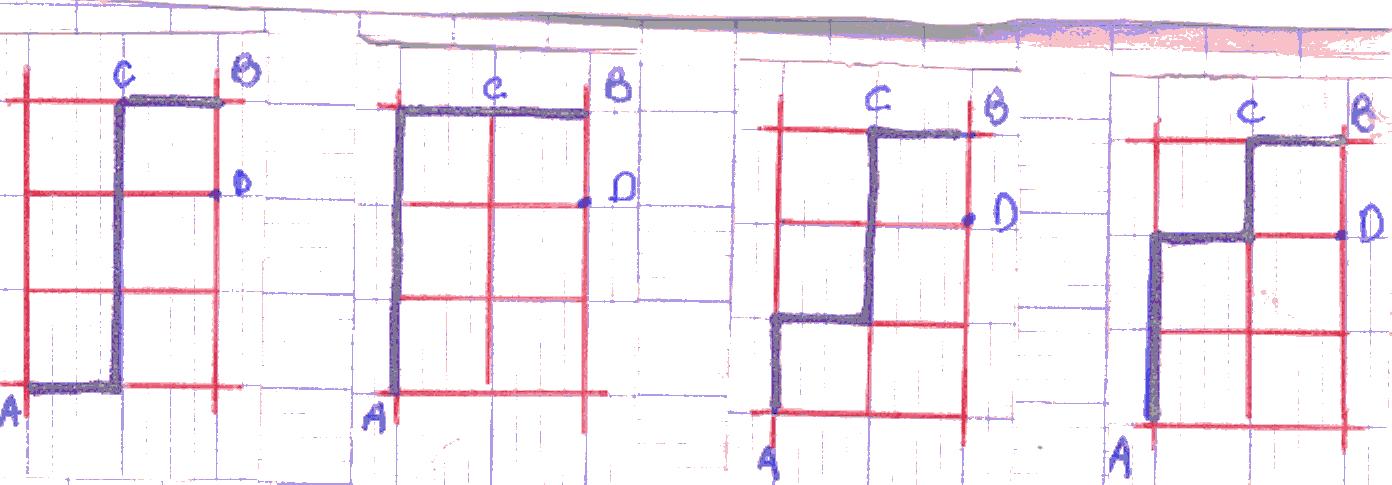
Commentaire. Les [L'ensemble des] 10 chemins pour aller à (2;3) [est formé par] la réunion [de l'ensemble] des 4 chemins pour aller à (1;3) [(au point C, voir figure 4, ci-dessous)] et [de l'ensemble] des 6 chemins pour aller à (2;2) [(au point D, voir figure 5, ci-dessous)]

En général [Partant de l'origine,] pour arriver au point (x,y), [avec x et y positifs] il faut passer par (x-1,y) ou par (x,y-1). Donc [Théorème 1] Pour obtenir le nombre de chemins pour aller à (x,y) [avec x et y positifs], il faut ajouter le nombre de chemins pour aller à (x-1,y) et le nombre de chemins pour aller à (x,y-1). [Il n'est pas difficile de compléter ce théorème pour les points de la forme (x,0) ou (0,y) : - pour x positif ou nul, un seul chemin permet d'aller à (x,0), - pour y positif ou nul, un seul chemin permet d'aller à (0,y), ]

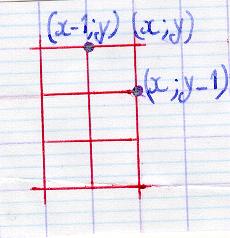Résultats des chemins sur un réseau carré

[En appliquant le théorème 1 on obtient le tableau suivant.]

1	8	36	120	330	792	1716	3432	[Les cases du tableau représentent les cases du quadrillage. L'origine étant prise le coin inférieur gauche du tableau, on peut faire correspondre à chaque case du quadrillage son coin inférieur gauche,Le contenu de chaque case représente alors le nombre de chemins "croissants" (c'est à dire formés de pas vers le haut ou vers la droite) qui vont de l'origine au coin inféreieur gauche de cette case. On vérifie bien le théorème 1, Le contenu des cases de gauche ou des cases inférieures vaut 1. Le contenu des autres cases s'obtient en ajoutant les contenus des deux cases situées à gauche et au dessous]
1	7	28	84	210	462	924	1716
1	6	21	56	126	252	462	792
1	5	15	35	70	126	210	330
1	4	10	20	35	56	84	120
1	3	6	10	15	21	28	36
1	2	3	4	5	6	7	8
1	1	1	1	1	1	1	1

Le défaut de cette méthode c'est que pour trouver un nombre du tableau il faut d'abord trouver les nombres précédents (exemple : pour trouver 35 il faut d'abord trouver 15 et 20). Comme c'est compliqué, nos camarades ont cherché puis trouvé une méthode... [la réponse de nos camarades est donnée en annexe]