Comptes Rendus MATh.en.JEANS 00-10 

Jumelage MATh.en.JEANS entre les collèges Robespierre (93800 Épinay sur Seine) et Elsa Triolet (93200 St Denis), année scolaire 1999-2000 (ateliers scientifiques).
Enseignants : Jean-Pierre BOURBOUZE (clg. Robespierre) et Claire DUMONT (clg. Elsa Triolet)
Chercheur : Benoît Rittaud (Institut Galilée, Villetaneuse)

 

---

[Article vérifié et commenté : les passages entre crochets sont des éditeurs]

[Préambule]

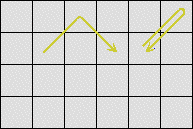
On considère un écran d'ordinateur ou de télévision composé de pixels [note 1]. Un point lumineux s'y déplace en diagonale [à 45°]. Quand il arrive dans le coin de l'écran il fait demi-tour et lorsque il arrive sur le bord de l'écran il continue sur l'autre diagonale [voir Figure 1]. On a représenté l'écran par un rectangle (ou un carré) et les pixels par des [petits] carrés semblables [égaux]. On obtient ainsi un quadrillage régulier du rectangle.

[] [Figure 1]

[ Au début un pixel s'allume, puis ce point lumineux se déplace dans une direction donnée, en rebondissant sur les parois, comme si l'écran était un billard.  Le sujet de recherche initial proposait d'étudier les trajets possibles : le point lumineux peut-il parcourir tout l'écran ? La trajectoire sera-t-elle longue, courte ? Qules pixels seront atteints ? Au bout de combien de temps ? Combien y en aura-t-il ? etc.
Les résultat présentés ici portent sur le nombre de trajectoires différentes possibles.]

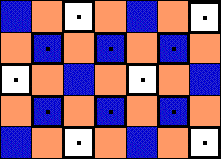
Le rectangle 3x7 représentera le rectangle de largeur 3 et de longueur 7 côtés lorsque l'unité utilisée est le [coté du] carreau ([plus généralement] nous noterons axb où a est la plus petite mesure du rectangle). Nous avons ici (figure 2) trois trajectoires différentes : l'une bleu, l'autre bleu clair et la dernière [avec des carreaux] encadrés.

Figure 2

Nous appelons trajectoire le chemin suivi par un point lumineux jusqu'à ce qu'il retourne à son point de départ [de façon qu'il refasse indéfiniment le même trajet : voir note 2].

Pour qu'une trajectoire se finisse [note 2] il faut que :

• Soit le point lumineux arrive dans un coin (dans ce cas il rebrousse chemin)
• Soit qu'elle forme une boucle fermée.

Nous avons établi trois résultats : le nombre de trajectoires pour un carré, un encadrement du nombre de trajectoires dans un rectangle et enfin le nombre de trajectoires pour un rectangle de côté 2.

Nous avons tout d'abord fait deux [trois] remarques essentielles pour la suite de nos déductions :

• [(1) Tout point lumineux décrit une trajectoire (voir note 3)]
•  (2) Tout rectangle peut être recouvert par un nombre fini de trajectoires [voir note 3].
•  (3) Quelque soit le point de départ que l'on prenne sur une trajectoire, cette dernière ne change pas. Ce qui veut dire que l'on peut restreindre notre raisonnement à l'étude des trajectoires démarrant sur les bords du rectangle.

1) Le Carré.

On note n la longueur du côté du carré.

On note k la distance séparant D et I. On veut montrer que JB = BT = LD = DI = k.

Calcul de IJ : Comme (IJ) // (DB) on utilise le théorème de Thalès , on obtient alors :

En utilisant la première égalité, on a :

donc AJ = n - k

et par suite JB = AB-AJ = k.

Par la symétrie d'axe (DB) on obtient : LD = k et TB = k.

On a ainsi prouvé que chaque trajectoire touche exactement une fois chaque côté du carré. La deuxième remarque énoncée en préambule nous permet de dire que l'on a le même nombre de trajectoire que de pixels sur un côté du carré.

[Theorème 1] Dans un carré de côté n pixels il y a exactement n trajectoires.

2) Le Rectangle

On considère un rectangle de mesures axb où  ab.

Lorsque le point lumineux démarre de l'un des coins du rectangle il arrive, en bout de trajectoire, dans un autre coin (en effet c'est la seule solution pour que la trajectoire soit finie [note 4]), à ce moment là le point lumineux fait demi-tour et passe par les mêmes pixels.

Une trajectoire partant d'un coin n'en atteint alors qu'un autre. Comme un rectangle comprend quatre coins on peut affirmer qu'il y a au moins deux trajectoires dans un rectangle.

Un trajectoire dans un rectangle touche obligatoirement les quatre côtés au moins une fois. Étant donné que le plus petit côté contient a pixels, on peut alors affirmer qu'il y a au plus a trajectoires.

[Theorème 2.] Dans un rectangle de mesures  ax b (ab) il y a au moins 2 trajectoires et au plus a trajectoires.

[Corollaire.] Dans un rectangle de largeur 2 il y a exactement 2 trajectoires.

[Preuve. Il y en a] au plus 2 et au moins 2 [d'après le théorème précédent].

[Malgré son caractère imprécis, la conclusion du théorème 2 ne peut être améliorée à peu de frais (voir note 5) ; la recherche continue... (cf. note 6)].

1. « Une image sur écran se compose d'un nombre fini de très petites surfaces toutes semblables, indivisibles qui selon l'information fournie à l'écran s'allument ou ne s'allument pas. Cette surface s'appelle le pixel. Selon le nombre de pixels qui composent une surface-écran, l'écran a une "définition" plus ou moins grande. » [Extrait de MARCHE: la géométrie du pixel par Michaël Arditti, David Benoun, Jean-Michel Chau et Soung Ngo du Lycée Racine de Paris, Actes MATh.en.JEANS1992 pp. 152-154.

retour au texte

2. Dans l'usage courant (en Mécanique et Mathématiques des "systèmes dynamiques") le mot trajectoire désigne plus généralement l'espace parcouru par un point mobile. Lorsque le mouvement est périodique, c'est à dire se reproduit à l'identique à intervalles de temps réguliers, on dit que la trajectoire est périodique. Ce sont ces trajectoires périodiques que les auteurs nomment simplement "trajectoire finies" ou simplement "trajectoires". En fait, dans le cas étudié ici (déplacements diagonaux avec un nombre fini de pixels) toutes les trajectoires sont périodiques (voir l'explication de la note 3).

retour au texte

3. Avec le langage de la note 2, la remarque (1) s'énonce sous la forme : toute trajectoire est périodique. Cette propriété est une hypothèse qui justifie la remarque (2).
On peut prouver la remarque (1), en prouvant que la situation de départ d'un point lumineux mobile (suivant les directions diagonales) se reproduit nécessairement :

(a) On observe que l'on peut "reconstruire le passé" dès que l'on connaît la situation du point lumineux à un moment donné, c'est à dire dès que l'on connaît sa position et sa direction de déplacement : en effet, il suffit d'inverser le sens du déplacement.
(b) Comme le nombre total de situations possibles est fini, un point lumineux mobile finit toujours par retrouver une situation dans laquelle il a déjà été.
(c) Appelons alors S la situation qui se reproduit pour la première fois, et appellons S^- la situation qui a immédiatement précédé cette répétition. Si S n'était pas la situation de départ, on voit, en appliquant (a), que la situation S^- se serait répétée avant S : c'est absurde. Donc S est la situation de départ ! CQFD.

retour au texte

4. Le fait que cette trajectoire soit "finie" (autrement dit périodique cf. note 2) résulte de la remarque (1) faite plus haut.

retour au texte

5. Voici deux exemples.

Figure 4 : Il ya 2 trajectoires dans le rectangle 3x8

Figure 5 : dans le 5x7 il y a 3 trajectoires : l'une en bleu, l'autre couleur parme, les cases de la troisième sont à la fois pointées et entourées.

6. On peut également se demander si les résultats de l'article s'étendent au cas continu, c'est à dire aux rectangles du plan composé de points géométriques et non plus de pixels. Les trajectoires inclinées à 45° y sont-elles encore fermées ?

retour au texte

Quelques références.

Dans sa version continue, le problème général du billard mathématique consiste à étudier le parcours d'un rayon de lumière qui se réfléchit indéfiniment sur le bord d'une forme plane donnée (rectangle, triangle, cercle, haricot avec éventuellement des obstacles). Sera-t-il ou non fermé ? Quels points atteindra-t-il ? Tout cercle intérieur sera-t-il atteint ? Toute portion du bord sera-t-elle touchée ? Sur ce thème, on peut consulter l'article "billards lumineux" par des lycéens des lycées Buffon et La Fontaine, publié dans les Actes MATh.en.JEANS 1996, pp.131-139, ainsi que la conférence de Jean-Christophe Yoccoz au 13^ème congrès MATh.en.JEANS (Orsay 23-25 mars 2002) dont le texte sera publiée fin 2002. Sur le cas du cercle, voir Le billard circulaire, par des élèves des lycées Charles Poncet (74-Cluses) et Camille Sée (Paris, 15) en 2000-2001, Comptes Rendus MATh.en.JEANS n° 01-07

Mots clefs

billard diagonale période pixel rectangle trajectoire.

Comptes Rendus MATh.en.JEANS 00-10

© MATh.en.JEANS 2002. Tous droits réservés.