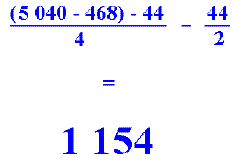Les déboires d'un carreleur,
Comptes Rendus MATh.en.JEANS 00-06
Annexes et notes des auteurs
1. La cuisine de Jean-Pierre:
démonstration
[Il s'agit de prouver l'énoncé suivant : si le
carrelage d'un rectangle mxn est possible avec des carreaux
1x3, alors l'un des nombres
m ou n au moins est un multiple de 3]
L'explication par l'aire: un rapport s'établit simplement entre l'aire
de la cuisine et l'aire des carreaux dont il se servira.
On a alors l'aire de la pièce,
m.n, qui sera
égale, quand la cuisine est carrelable, à l'aire d'un
carreau 1x3 multiplié par
le nombre de carreaux utilisés, que l'on notera
k.
Ce qui nous donne: m.n = 3.k
3 étant un
nombre premier, on peut déduire de cette
égalité les deux suivantes:
m = 3.k
et [ou] n =
3.k
[explication en NdE 1]
Conclusion: pour que la cuisine soit
carrelable, il faudra que ses dimensions vérifient l'une ou
l'autre de ces relations.
retour au texte
2. Nombre premier
Un nombre premier est un
nombre [entier positif différent de 1] qui n'est divisible que par 1 et par
lui-même.
Exemples: 1 [par
convention 1 n'est pas considéré comme nombre
premier], 3, 5, 7, 11, 13 Š
retour au premierappel de
cette note
3. Conjecture.
Une conjecture est un
résultat que l'on pense être juste d'après de
nombreux exemples, mais qui n'est pas démontré.
retour au premierappel
de cette note
4. La salle de bains de Jean-Pierre :
démonstration.
De la même façon que
pour la
cuisine (vers lien 5), on peut
retrouver une relation entre l'aire de la salle de bains et l'aire
des carreaux.
Soient m et n les
côtés de la salle de bains, p la longueur du
carreau et k un nombre entier positif quelconque.
Si p est un nombre
premier :
On montre de la même manière (cf. démonstration pour la cuisine
et NdE 1] qu'il faut que m ou n soient des multiples de
p.
Si p
est un nombre non premier.
Nous avons seulement établi une conjecture...: il faudrait que m ou n soient des multiples de p mais
nous ne sommes pas parvenus à le démontrerŠ[pour un énoncé
précis de cette conjecture voir NdE 2]
retour au texte
5. Nombre de configurations.
Nombre de possibilités de placer les
pièces noires [en respectant la condition "il ne faut
qu'un carreau noir par ligne et par colonne"].
|
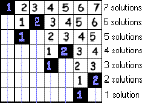
[Exemple : Il y aura une case noire par ligne. Il ya 7
manières de placer une case noire sur la
première ligne, on en choisit une, la position 1 par
exemple. Il reste alors 6 manières de placer la case
noire de la seconde ligne : on en choisit une, la position 2
par exemple. Et ainsi de suite...]
|
|
Il y a donc 7 x
6 x 5
x 4 x 3 x
2 x 1 façons de placer les cases noires.
Cela se note
7 ! (lire :
« factorielle
7 »), qui est égale à :
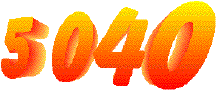
retour au texte
6. Coin bouché.

retour au texte
7. Nombre de configurations ayant un coin
bouché.
Si on bouche un coin avec deux cases noires,
on sait qu'il n'y aura pas d'autres cases noires dans les deux lignes
et les deux colonnes dans lesquelles elles se trouvent.
On peut donc, pour trouver le nombre de
configurations ayant un coin bouché, chercher le nombre de
façons de placer les cases noires dans un carré de
5x5.

Là, de la même façon que
pour le nombre de
configurations totales, on trouve
qu'il y aura 5 x4 x3 x2 x1
configurations ayant le coin supérieur gauche bouché.
Cela se note 5 ! (lire « factorielle
5 ») et est égal à 120.
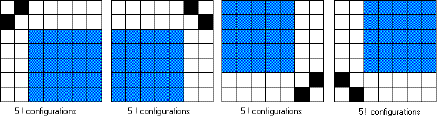
Chaque coin pouvant être bouché
tour à tour:
Il y a donc logiquement 4 x5!
soit 480 configurations ayant un coin bouché.
Mais des configurations ont
été comptées deux fois!
En effet, certaines configurations ayant
deux coins bouchés, nous les avons comptées pour chacun
de leur coin bouché, soit deux fois. Pour les
dénombrer, nous nous sommes cette fois ramené à
un carré de 3 x3 et avons
procédé toujours de la même manière que
pour le nombre de configurations totales [voir plus haut]:
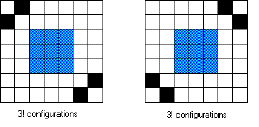
Il y a 2 x3!
soit 12 configurations que nous devons retirer des 480
comptées précédemment, cela nous amène
donc à 480-12 soit:
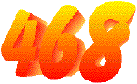
configurations ayant un coin
bouché.
retour au texte
8. Configurations n'existant que de deux
façons par rotation
Les configurations qui, par rotation, ne
donneront que deux cas différents sont celles qui ont la
particularité d'avoir leur cases noires disposées
symétriquement par rapport au carreau central:
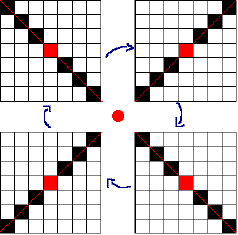
Pour les dénombrer, nous avons
à nouveau étudié le nombre de
possibilités de placer les cases noires dans chaque ligne, en
commençant par la case centrale, puis en disposant au fur et
à mesure le symétrique des cases que l'on aura
placé:
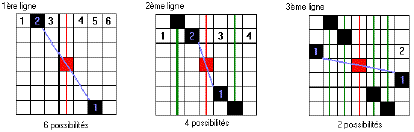
Nous avons donc 6 x4 x2 possibilités,
soit 48 possibilités pour placer les cases de façons
à ce qu'elles soient symétriques par rapport au carreau
central.
Mais si vous avez bien suivi, vous avez du
remarquer que certaines d'entre elles allaient avoir un coin
bouché, et que par conséquent elles ne faisaient
déjà plus partie des 4572 configurations auxquelles
nous étions parvenus. Un petit dessin nous a à nouveau
permis de les dénombrer:
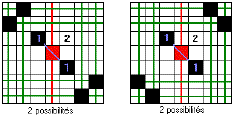
Cela nous fait 2+2 soit 4 configurations
dont on ne "s'occupe" plus parmi les 48.
Il y a donc:

configurations parmi les 4572 que l'on ne
divisera que par 2.
retour au texte
9. Le savant calcul.
Récapitulatif pour ceux qui ont pas
tout suivi:
Nous avons tout d'abord
dénombré 5 040 manières possibles de placer les
carreaux noirs sur la terrasse de René.
Ne pouvant raisonnablement pas
étudier le pavage de chaque cas durant cette année,
nous avons tenté de diminuer ce nombre, tout d'abord en
éliminant des cas que l'on sait non pavables: les
configurations ayant un coin bouché. Il y en a 468, il nous
reste donc:
5 040 - 468
= 4572 configurations
à étudier
Vient ensuite la constatation que l'on peut
diviser ce nombre par 4 grâce au "phénomène" de
rotation, mis à part 44 cas parmi ces 4572 que l'on ne
divisera que par 2 parce qu'ils ne donnent que deux configurations
différentes. Cela nous donne donc:
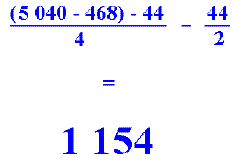
retour au texte
|
Comptes Rendus
MATh.en.JEANS 00-06
|
© MATh.en.JEANS 2001. Tous droits réservés.
|