Relier chaque ville à 3 villes :

Le nombre minimum de villes est 4. On relie chacune des 4 villes à 3 villes :

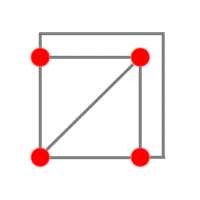
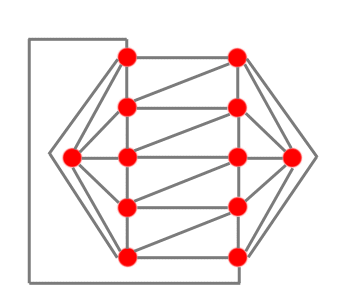
Puis pour 6 villes :

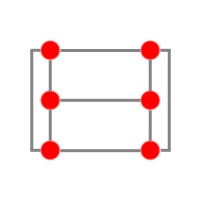
A partir de ce schéma, on va pouvoir rajouter deux villes :

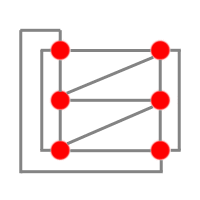
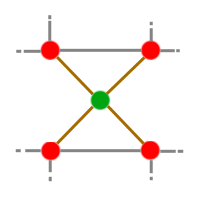
Considérons le schéma précédent :

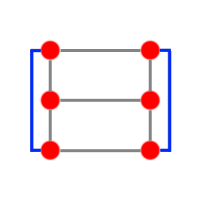
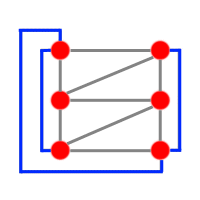
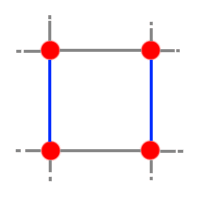
On retire d'abord les 2 autoroutes bleues :

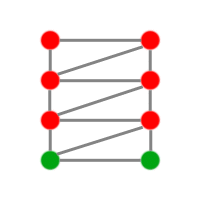
Ensuite on ajoute 2 villes vertes que l'on relie aux 2 villes qui sont au-dessus :

On rétablit ensuite les anciennes autoroutes bleues :

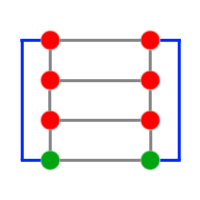
On obtient alors un schéma à 8 villes reliées chacune à 3 villes.

Comme on va toujours pouvoir rajouter deux villes, il sera possible de relier chaque ville à 3 villes pour tout nombre pair (et supérieur ou égal à 4) de villes.

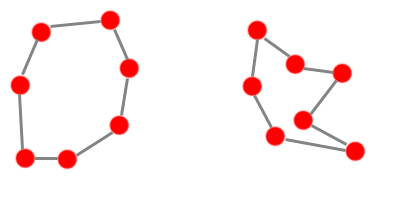
Voyons ce qui se passe avec un nombre impair de villes :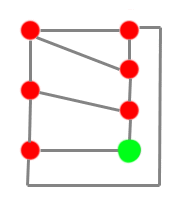

Ca ne marche pas. Afin de savoir pourquoi cela ne marche pas, nous allons nous aider de la formule suivante :

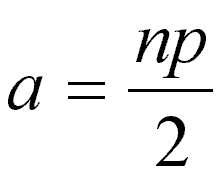
où a est le nombre d'autoroutes, n le nombre de villes et p le nombre de villes auxquelles chaque ville est reliée.

Pourquoi cette formule ? On cherche à connaître le nombre d'autoroutes. Chacune des n villes est reliée à p villes. On forme donc le produit np. Mais comme chaque autoroute est partagée entre 2 villes, nous avons compté 2 fois trop d'autoroutes. D'où la formule ci-dessus.

Revenons à notre problème, qui est de relier 5 villes à 3 villes. On a : . a n'est alors pas entier. Or a représente le nombre d'autoroutes; il est donc nécessairement entier. C'est pourquoi il est impossible de relier 5 villes à 3 villes. Nous pouvons généraliser ce résultat : en effet il sera impossible de relier un nombre impair de villes à un nombre lui aussi impair de villes, car on aurait alors un numérateur impair qui, divisé par 2, ne donnerait pas un entier.

Relier chaque ville à 4 villes

Commençons avec les nombres pairs de villes. On peut voir, lorsque l'on souhaite relier chaque ville à toutes les autres, qu'il est impossible de relier 5 villes entre elles (donc de relier 5 villes à 4 villes).

Voyons donc pour 6 villes :

A partir de ce schéma, on va pouvoir rajouter 2 villes (on utilise la même méthode que pour ajouter 2 villes quand on souhaite relier chaque ville à 3 villes) :

Considérons le schéma précédent :

On retire d'abord les 3 autoroutes bleues :

Ensuite on ajoute 2 villes vertes que l'on relie aux 2 villes qui sont au-dessus :

On rétablit ensuite les anciennes autoroutes bleues :

On obtient alors un schéma à 8 villes reliées chacune à 4 villes.

 

Comme il est toujours possible de rajouter deux villes, on va pouvoir relier tout nombre de villes pair et supérieur à 6 à 4 villes.

 

Voyons maintenant ce qui se passe pour un nombre impair de villes.

Nous avons trouvé une méthode permettant de rajouter 1 ville à certains schémas, sans pour autant changer ses propriétés.

Des conditions sont nécessaires pour pouvoir ajouter une ville : il faut pouvoir isoler un quadrilatère vide formé par les autoroutes de la figure :

 

On supprime alors deux autoroutes n'aboutissant pas à la même ville (par exemple, les 2 autoroutes bleues) :

 

On peut alors ajouter la nouvelle ville (verte) que l'on relie aux 4 villes, extrémités des autoroutes supprimées :

On obtient alors un schéma à n+1 villes reliées à 4 villes.  

Cette méthode nous permet de rajouter une ville à un schéma où l'on avait relié un nombre pair et supérieur ou égal à 8 de villes à 4 villes. En effet, sur un schéma à 6 villes, on n'observe que des triangles :

 

CONCLUSION :

On peut relier chaque ville à :

2 villes pour tout nombre de villes au moins égal à 3;

3 villes pour tout nombre de villes pair et supérieur ou égal à 4;

4 villes pour 6 villes et pour tout nombre de villes supérieur ou égal à 8;

5 villes si le nombre de villes est 12.