Sujet proposé
Paul et Virginie aiment jouer à la marelle, mais ils en ont changé les règles [note 1]. On part de la TERRE pour aller au CIEL en passant par 4 cases numérotées de 1 à 4. La règle est la  suivante: sur chaque case, le joueur lance une pièce. Si la pièce tombe sur " pile ", le joueur reste sur place. Si elle tombe sur " face ", le joueur avance d'une case. Comme on a une  chance sur deux d'avancer, Virginie parie qu'en au plus de 10 coups, elle arrivera au CIEL.

• Qu'en pensez-vous? Imaginer d'autres règles et d'autres paris (par exemple avec des dés ou avec une pièce truquée ou si la piste de jeu est un échiquier.
  

Commentaire
Nous avons décidé qu'une marelle à 4 cases, c'était trop compliqué pour compter alors pour faciliter le jeu, nous avons donc pris seulement 2 cases.

Pour 7 Lancers

Tableau de simulation

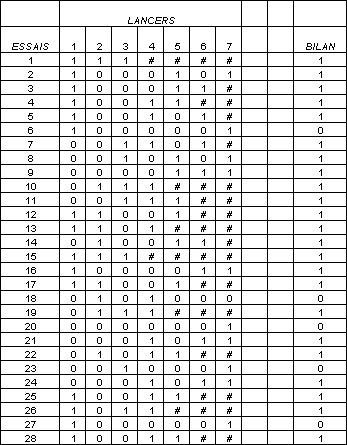
C'est un tableau qui représente le bilan d'un jeu de marelle qui comporte les cases: TERRE, UN, DEUX et CIEL.   Le tableau comporte : 7 lancers. 1000 essais. Ce tableau consiste à savoir si c'est facile d'arriver au CIEL.   A chaque essai : - il apparaît un 1 si nous avançons d'une case. - il apparaît un 0 si nous n'avançons pas d'une case - il apparaît un # si nous avons trois 1 sur la ligne et au bout de trois 1, ça veut dire que nous avons gagné donc nous mettons un 1 dans la case du bilan.

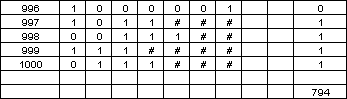
Au bout de 1000 essais, il y a 794 réussites (nous sommes arrivés au ciel). Donc nous obtenons environ 79% de réussite.

...

L'arbre

Document annexe 1

Construction de l'arbre

L'arbre est fait comme un arbre généalogique. Il est présenté avec des cases et des branches. Les cases sont constituées :

de Terre, de 1, de 2 et de Ciel.

Au début, la première case est Terre. Elle est reliée par deux branches à deux cases : Terre et 1 et ainsi de suite.

Première méthode pour compter le nombre de réussites par rapport au nombre de possibilités.

Nous avons compté tous les ciels et toutes les possibilités qu'il y avait sur l'arbre à la fin des branches. Nous avons divisé le nombre de ciels par le nombre de possibilités.

Nous avons trouvé 63 possibilités, et sur ces 63 possibilités, il y a 35 ciels. Nous avons divisé 35 par 63 ce qui donne 0,55 ou 55%.

Nous avons comparé le résultat calculé au résultat du tableau et nous nous sommes aperçus que cela n'allait pas. Donc nous avons recommencé une autre fois en faisant une autre méthode.

Deuxième méthode pour compter le nombre de réussites par rapport au nombre de possibilités.

Pour chaque branche qui se termine par ciel avant le 7ème lancer, nous la continuons jusqu'au 7ème lancer. Puis nous comptons tous les ciels.

Nous avons trouvé 128 possibilités,et sur ces 128 possibilités, il y a 99 ciels. Nous avons divisé 99 par 128 ce qui donne environ 0,77 ou 77%.

Conclusion

La 2éme méthode est celle qui se rapproche le plus du tableau de simulation, donc c'est celle que nous avons adoptée.

Pour 7 lancers, nous avons 77% de réussite. Nous ne sommes pas sûrs de gagner.

Pour 8 Lancers

Tableau de simulation

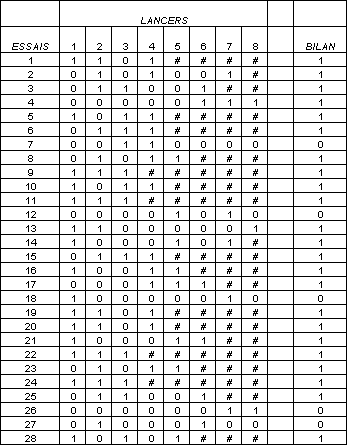
C'est un tableau qui représente le bilan d'un jeu de marelle qui comporte les cases: TERRE, UN, DEUX et CIEL.   Le tableau comporte : 7 lancers. 1000 essais. Ce tableau consiste à savoir si c'est facile d'arriver au CIEL.   A chaque essai : - il apparaît un 1 si nous avançons d'une case. - il apparaît un 0 si nous n'avançons pas d'une case - il apparaît un # si nous avons trois 1 sur la ligne et au bout de trois 1, ça veut dire que nous avons gagné donc nous mettons un 1 dans la case du bilan.

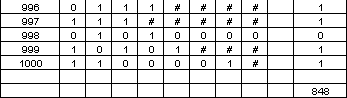
Au bout de 1000 essais, il y a 848 réussites (nous sommes arrivés au ciel). Donc nous obtenons environ 85% de réussite.

...

L'arbre

Construction de l'arbre : l'arbre est fait comme un arbre généalogique. Il est présenté avec des cases et des branches. Les cases sont constituées :

de Terre, de 1, de 2 et de Ciel

Au début, la première case est Terre. Elle est reliée par deux branches à deux cases: terre et 1 et ainsi de suite.

Première méthode pour compter le nombre de réussites par rapport au nombre de possibilités :

Nous avons compté tous les ciels et toutes les possibilités qu'il y avait sur l'arbre. Nous avons divisé le nombre de ciels par le nombre de possibilités.

Nous avons trouvé 92 possibilités, et sur ces 92 possibilités, il y a 56 ciels. Nous avons divisé 56 par 92 ce qui donne 0,60 ou 60%.

Nous avons comparé le résultat calculé au résultat du tableau et nous nous sommes aperçus que cela n'allait pas.

Donc nous avons recommencé une autre fois en faisant une autre méthode.

Deuxième méthode pour compter le nombre de réussites par rapport au nombre de possibilités :

Pour chaque branche qui se termine par ciel avant le 8ème lancer, nous la continuons jusqu'au 8ème lancer. Puis nous comptons tous les ciels.

Nous avons trouvé 256 possibilités, et sur ces 256 possibilités, il y a 219 ciels. Nous avons divisé 219 par 256 ce qui donne environ 0,86 ou 86%.

Conclusion

La 2éme méthode est celle qui se rapproche le plus du tableau de simulation, donc c'est celle que nous avons adoptée.

Pour 8 lancers, nous avons 86% de réussite. Nous sommes presque sûrs de gagner.

Pour 9 et 10 lancers.

Méthode de calcul

Les arbres devenant de plus en plus importants, nous allons chercher une formule de calcul pour le nombre de possibilités et le nombre de ciels.

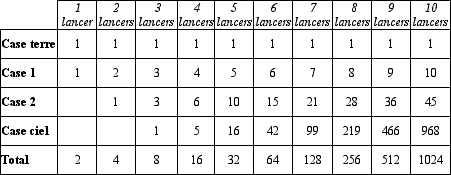
Pour la case terre et quel que soit le nombre de lancers nous obtenons 1 fois terre. Pour la case 1, chaque résultat est égal au nombre de lancers. Pour la case 2, nous obtenons le résultat en faisant une addition avec le nombre de cases 1 et le nombre de cases 2 du lancer précédent. Pour la case ciel, nous obtenons le résultat en faisant une addition avec le nombre de cases 2 et le double du nombre de cases ciel du lancer précédent.

Conclusion

Pour 9 lancers, nous avons trouvé 512 possibilités, et sur ces 512 possibilités, il y a 466 ciels. Nous avons divisé 466 par 512 ce qui donne environ 0,91 ou 91 % de réussite.

Pour 10 lancers, nous avons trouvé 1024 possibilités, et sur ces 1024 possibilités, il y a 968 ciels. Nous avons divisé 968 par 1024 ce qui donne environ 0,95 ou 95% de réussite.

Nous sommes pratiquement sûrs de réussir à partir de 9 lancers.

1. <<  L'origine de la marelle demeure mystérieuse. Dès 2357 avant J.-C., des textes chinois en font mention. Dessiné sur des sépultures en Égypte, en Grèce ou ailleurs dans le monde, ce jeu à tableaux offre toujours le même tracé rectangulaire ou en spirale.

[ voir Une petite fille jouant à la marelle dans la cour de l'École des Ursulines de Québec.]

Le joueur progresse à cloche-pied en poussant un palet qui représente l'âme. S'il boite, c'est que son âme est faible et qu'il doit s'astreindre à des efforts purificatoires pour gagner son ciel. Après avoir évité l'enfer et remporté différents mérites, il atteint le paradis, récupère le palet (son âme) et le place sous son bras ou sur sa tête, faisant réintégrer l'âme au corps. Le jeu de marelle consiste à ne pas poser le pied sur les lignes qui divisent les cases. Cette règle correspond symboliquement au besoin de se mettre à l'abri de l'incertitude. Dans la marelle, tout est prévisible. Jeu initiatique, il révèle l'individu à lui-même en développant certaines de ses capacités. De la marelle inscrite au sol, on passe à celle que l'on dessine sur une surface plane. La marelle est l'ancêtre des jeux à tableaux (go, échecs, dames, etc.) appelés « marelles assises ».  >>

retour à l'appel de cette note

PROBABILITÉS MODÉLISATION MODÈLE MARELLE ARBRE DES POSSIBILITÉS STATISTIQUE