Comptes Rendus MATh.en.JEANS 01-03

Dames sur un échiquier

 

Cet article a été rédigé par : AAA (ne souhaite pas que son nom soit publié), Sébastien THALOT et Kevin LASCAR
élèves du collège l'ardillière de Nézant à Saint-Brice sous Forêt (val d'oise),
aidés de leurs professeurs M.BOURIT Yann et M.MARTINOD Eric.
Cette recherche a été menée en parallèle avec des élèves du collège Charles LEBRUN à Montmorency (val d'oise):
Fabien OZIL, Philippe SALLENAVE, Jordan BEN OLIEL, Elodie DOS SANTOS, Anaïs PETRONE? Violette ESNEE, Charlotte BURY et Fabian GRISLAIN,
aidés de leurs professeurs M.GEORGES Christian et M. ALBERTINI Frédéric .
Les deux équipes de chercheurs en herbe étaient chapeautées par :
M. VIDAL Julien, chercheur au Groupe de Physique des Solides, CNRS UMR 7588, Universités Paris 6 et Paris 7.

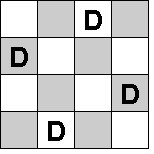
Combien peut-on mettre de dames sur un échiquier de nxn cases sans qu'elles se mangent les unes les autres ?

Pour le 1x1, on met une dame, évidemment.

Sur le 2x2, on ne peut en mettre qu'une, également. Sur le 3x3, on peut en mettre 2.

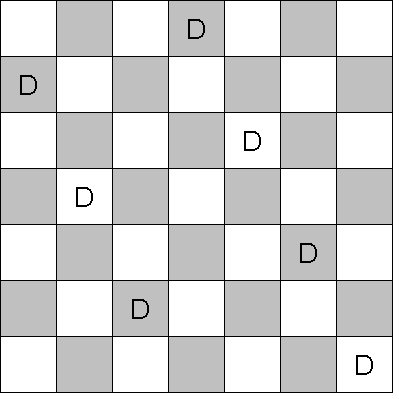
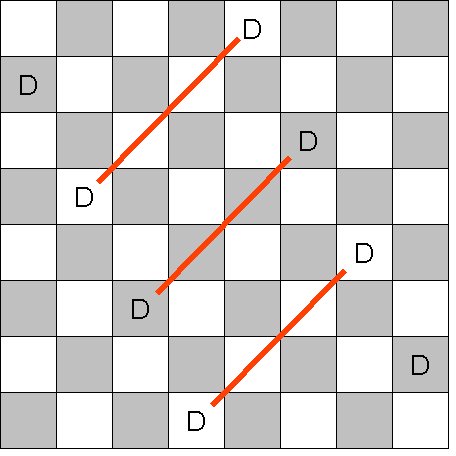
Nous sommes partis sur l'idée de tracer des "droites de cavaliers": on part de la case (2;1), et on descend comme un cavalier: une case vers la droite et deux cases vers le bas. Quand on ne peut plus aller plus bas, on remonte à la première ligne en se décalant d'une colonne. Et on redescend comme un cavalier.

Sur un 4x4, on peut en mettre 4,

sur un 5x5, on peut en mettre 5.

 

.

Sur un 6x6, on peut en mettre 6

Sur un 7x7, on peut en mettre 7.

 

Nous nous sommes vite rendus compte d'une règle générale:

On ne peut pas mettre plus de n dames sur un échiquier nxn,

car on ne peut pas mettre plus d'une dame par ligne.

 

 

Mais patatras, sur le 8x8 il ne suffit pas de faire des droites, car la dame de (1;5) mange celle qui est en (4;2).

 

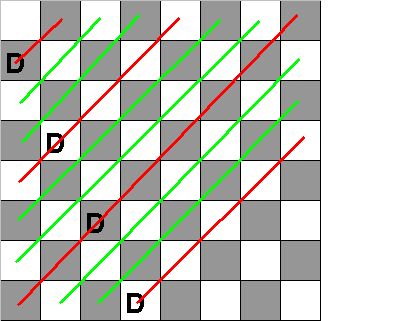
Alors, on a cherché quand la méthode des "droites de cavaliers" marchait. Et on a vu la chose suivante.

Entre deux dames qui se suivent, il y a deux diagonales libres ( lignes vertes ) alors que les dames de la première droite neutralisent une diagonale sur trois (lignes rouges).


Or, quand on agrandit l'échiquier, il faut rajouter deux lignes à l'échiquier pour que la dame de la première ligne se décale d'une case vers la droite.

Conclusion: La méthode des "droites de cavaliers" marche quatre fois sur six, pour 4, 5, 6 et 7 mais pas pour 8 ni pour 9. Elle remarche pour 10, 11, 12 et 13 mais pas pour 14 et 15...

 

Mais on a quand même trouvé une solution sur le 8x8.

 

 


A partir de cette solution, on en a trouvé d'autres :

Ce qui fait déjà 8 solutions.

Ensuite, on a eu l'idée de faire des permutations circulaires: on prend la colonne de gauche et on la met à droite.

 

Plus les 7 autres solutions par symétrie axiale et rotations de 90 degrés.

 

De même, on peut prendre la colonne de droite et la mettre à gauche.


Et on peut faire, à nouveau les rotations et symétrie pour avoir 7 autres solutions. Nous en sommes à 24.

De même, on peut prendre la ligne du bas et la mettre en haut:

 

 

Ce qui nous donne 8 nouvelles solutions. Nous en sommes donc à 32. Ce n'est sans doute pas terminé, mais nous nous sommes arrêtés là.

Défi: est-il possible de mettre 9 dames sur un échiquier de 9x9 cases ?

Nous avons essayé et nous n'avons (pas encore) réussi.

Comptes Rendus MATh.en.JEANS 01&endash;03

© MATh.en.JEANS 2001. Tous droits réservés.

Retour au   début de l'article

Retour aux Comptes Rendus MATh.en.JEANS