Réalisé par des élèves du lycée Henri Moissan de Meaux (77) :
            CHABREDIER Dorothée, DUCHAUSSOIS Gaëtan, ETIENNE Romain, GAILLARD Corinne
        Professeur : Mlle LEFRANC
        Chercheur : BODINI Olivier

[version préliminaire de l'article, avril 2000; les passages entre crochetssont des éditeurs]

    

         Nous devons construire un nouveau réseau de PIPE-LINES et y placer une raffinerie mais nous avons un budget réduit
         Comment placer les PIPE-LINES et où y placer la raffinerie pour dépenser un minimum d'argent.

      Introduction:
          Nous nous sommes fixés au départ comme règle qu'il devait y avoir un point de ralliement n'appartenant pas au tracé de la figure représenté par
        les pipe-lines.
          Nous avons débuté par des cas particuliers (démonstrations), avant d'essayer d'étendre à des généralités (que des conjectures hélas).

pour 2 points [lien manquant]

Démonstration pour deux points

Pour deux puits de pétrole, la meilleure solution est évidemment la ligne droite, la raffinerie R doit se trouver sur le pipe line entre les deux puits
 

pour une infinité de points alignés

Démonstration pour une infinité de points alignés

    Pour une infinité de points alignés , la plus courte distance est une ligne droite entre le premier point et le dernier point.
    Car le plus court chemin entre deux   points est la ligne droite
 
[Image manquante]

pour 3 points formant un triangle équilatéral [lien manquant]

 

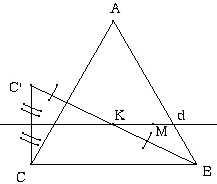
Démonstration pour 3 points formant un triangle équilatéral

 

Hypothèses:
 

_ ABC triangle équilatéral

_ M un point quelquonque

_ d la parallèle à (BC) passant par M

_ C' le symétrique de C par rapport à d

_ {K}=[BC']d 

 

Démonstration:

_AK<AM car AM hypothénuse de AKM rectangle en K.

_ BC'=BK+KC<BM+MC car la ligne droite est le plus court chemin entre deux points.

_ Dans BCC' K ets le milieu de [CC'] et Kd => D'après le théoreme des milieux, K milieu de BC' => KC'=KB=> KB=KC

=>K [appartient] à la médiatrice de [BC]

_ De même pour les deux autres cotés. 

 

Le point de concours pour que la distance soit la plus courte est le centre du cercle circonscrit dans un triangle équilatéral.

pour 3 points [lien manquant]

Conjecture: angles de 120°

 

- Pour trois Pipe-lines
Conditions : Aucun angle reliant deux Pipe-line ne doit être superieur à 120°.
 Le point qui relie les trois Pipe-lines au plus court, est  le point se trouvant entre deux Pipe-Lines avec un écartement de 120°. On obtient ainsi trois angles de 120° chacun.

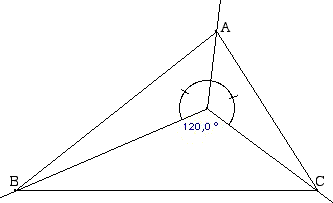  quand tout va bien

   quand un des angles est supérieur à 120°, ici â 

pour 4 points [lien manquant]

Conjecture avec 4 puits

Lemme: Si aucun des puits n'est aligné avec un autre, nous constatons que la figure obtenue est un quadrilatère.
Or, nous pouvons diviser un quadrilatère en au moins 2 triangles différents.

[Image manquante]
 

Test: Tentons donc la méthode vue auparavant concernant 3 puits de pétrole placés d'une manière quelconque sur ce quadrilatère divisé en 2 triangles.
Résultat: A chaque essai, nous avons constaté une longueur de pipe-lines utilisée inférieure aux longueurs précédemment obtenues par d'autres méthodes.
Conclusion : Il semblerait que diviser le quadrilatère en 2 triangles pour appliquer ensuite la solution obtenue pour 3 puits indifféremment placés à ces 2 triangles nous donne la solution optimale.

pour n points [lien manquant]

- Il en est de même pour n pipe-lines, il y a alors plusieurs point de rencontre

Ceci n'est pas démontré mais vérifié expérimentalement par mesure et par une maquette reproduisant un phénomène physique : Sur un bout de carton ou une feuille assez rigide, on fait trois trous. Puis on passe un bout de ficelle dans chaque trou et on fait un núud au dessus du support de tel manière à relier les trois ficelles. Ensuite, en dessous du support on fixe un poids d'égal masse au bout de chaque ficelle.
    On voit alors que le noeud est le sommet de trois angles de 120°.